Tag Archives: quantum games

Building a Visceral Understanding of Quantum Phenomena

Posted on by
1

A great childhood memory that I have comes from first playing “The Incredible Machine” on PC in the early 90’s. For those not in the know, this is a physics-based puzzle game about building Rube Goldberg style contraptions to achieve given tasks. What made this game a standout for me was the freedom that it granted players. In many levels you were given a disparate set of components (e.g. strings, pulleys, rubber bands, scissors, conveyor belts, Pokie the Cat…) and it was entirely up to you to “MacGuyver” your way to some kind of solution (incidentally, my favorite TV show from that time period). In other words, it was often a creative exercise in designing your own solution, rather than “connecting the dots” to find a single intended solution. Growing up with games like this undoubtedly had significant influence in directing me to my profession as a research scientist: a job which is often about finding novel or creative solutions to a task given a limited set of tools.

From the late 90’s onwards puzzle games like “The Incredible Machine” largely went out of fashion as developers focused more on 3D games that exploited that latest hardware advances. However, this genre saw a resurgence in 2010’s spearheaded by developer “Zachtronics” who released a plethora of popular, and exceptionally challenging, logic and programming based puzzle games (some of my favorites include Opus Magnum and TIS-100). Zachtronics games similarly encouraged players to solve problems through creative designs, but also had the side-effect of helping players to develop and practice tangible programming skills (e.g. design patterns, control flow, optimization). This is a really great way to learn, I thought to myself.

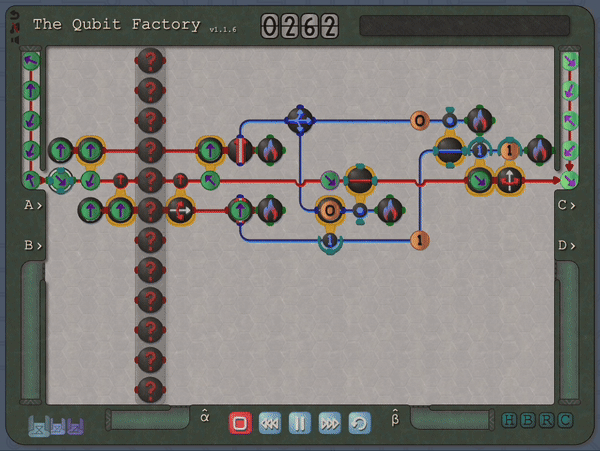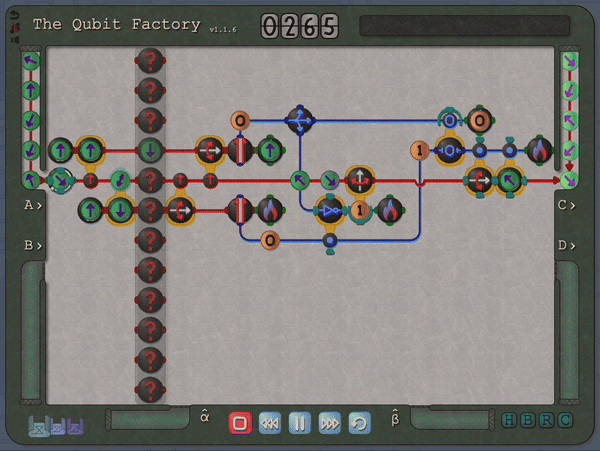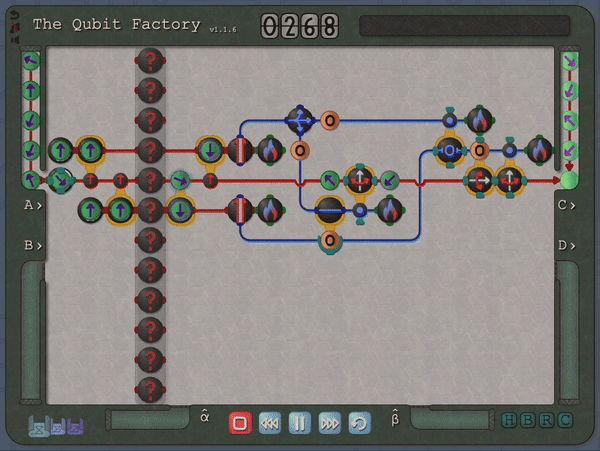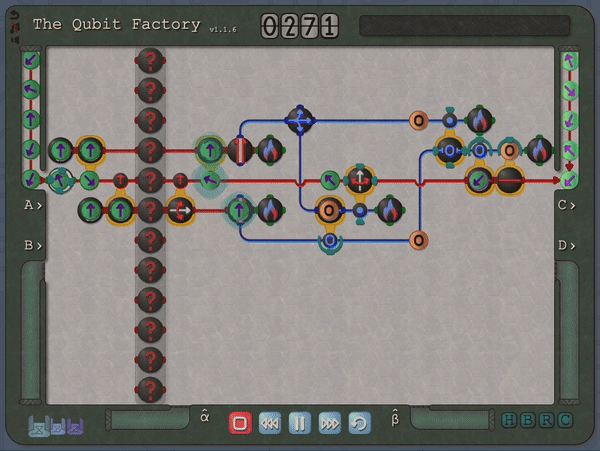
So, fast-forward several years, while teaching undergraduate/graduate quantum courses at Georgia Tech I began thinking about whether it would be possible to incorporate quantum mechanics (and specifically quantum circuits) into a Zachtronics-style puzzle game. My thinking was that such a game might provide an opportunity for students to experiment with quantum through a hands-on approach, one that encouraged creativity and self-directed exploration. I was also hoping that representing quantum processes through a visual language that emphasized geometry, rather than mathematical language, could help students develop intuition in this setting. These thoughts ultimately led to the development of The Qubit Factory. At its core, this is a quantum circuit simulator with a graphic interface (not too dissimilar to the Quirk quantum circuit simulator) but providing a structured sequence of challenges, many based on tasks of real-life importance to quantum computing, that players must construct circuits to solve.

An example level of The Qubit Factory in action, showcasing a potential solution to a task involving quantum error correction. The column of “?” tiles represents a noisy channel that has a small chance of flipping any qubit that passes through. Players are challenged to send qubits from the input on the left to the output on the right while mitigating errors that occur due to this noisy channel. The solution shown here is based on a bit-flip code, although a more advanced strategy is required to earn a bonus star for the level!

Quantum Gamification and The Qubit Factory

My goal in designing The Qubit Factory was to provide an accurate simulation of quantum mechanics (although not necessarily a complete one), such that players could learn some authentic, working knowledge about quantum computers and how they differ from regular computers. However, I also wanted to make a game that was accessible to the layperson (i.e. without a prior knowledge of quantum mechanics or the underlying mathematical foundations like linear algebra). These goals, which are largely opposing one-another, are not easy to balance!

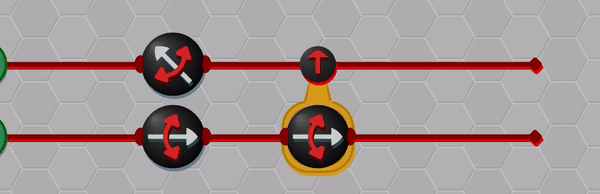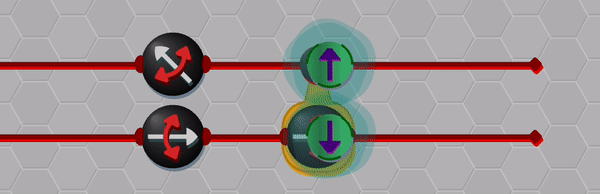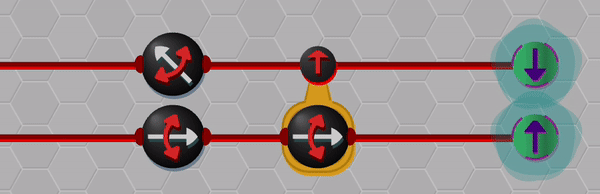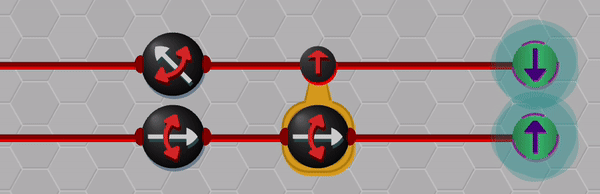
A key step in achieving this balance was to find a suitable visual depiction of quantum states and processes; here the Bloch sphere, which provides a simple geometric representation of qubit states, was ideal. However, it is also here that I made my first major compromise to the scope of the physics within the game by restricting the game state to real-valued wave-functions (which in turn implies that only gates which transform qubits within the X-Z plane can be allowed). I feel that this compromise was ultimately the correct choice: it greatly enhanced the visual clarity by allowing qubits to be represented as arrows on a flat disk rather than on a sphere, and similarly allowed the action of single-qubit gates to depicted clearly (i.e. as rotations and flips on the disk). Some purists may object to this limitation on grounds that it prevents universal quantum computation, but my counterpoint would be that there are still many interesting quantum tasks and algorithms that can be performed within this restricted scope. In a similar spirit, I decided to forgo the standard quantum circuit notation: instead I used stylized circuits to emphasize the geometric interpretation as demonstrated in the example below. This choice was made with the intention of allowing players to infer the action of gates from the visual design alone.

A quantum circuit in conventional notation versus the same circuit depicted in The Qubit Factory.

Okay, so while the Bloch sphere provides a nice way to represent (unentangled) single qubit states, we also need a way to represent entangled states of multiple qubits. Here I made use of some creative license to show entangled states as blinking through the basis states. I found this visualization to work well for conveying simple states such as the singlet state presented below, but players are also able to view the complete list of wave-function amplitudes if necessary.

\textrm{Singlet: }\left| \psi \right\rangle = \tfrac{1}{\sqrt{2}} \left( \left| \uparrow \downarrow \right\rangle - \left| \downarrow \uparrow \right\rangle \right)

A singlet state is created by entangling a pair of qubits via a CNOT gate.

Although the blinking effect is not a perfect solution for displaying superpositions, I think that it is useful in conveying key aspects like uncertainty and correlation. The animation below shows an example of the entangled wave-function collapsing when one of the qubits is measured.

A single qubit from a singlet is measured. While each qubit has a 50/50 chance of giving ▲ or ▼ when measured individually, once one qubit is measured the other qubit collapses to the anti-aligned state.

So, thus far, I have described a quantum circuit simulator with some added visual cues and animations, but how can this be turned into a game? Here, I leaned heavily on the existing example of Zachtronic (and Zachtronic-like) games: each level in The Qubit Factory provides the player with some input bits/qubits and requires the player to perform some logical task in order to produce a set of desired outputs. Some of the levels within the game are highly structured, similar to textbook exercises. They aim to teach a specific concept and may only have a narrow set of potential solutions. An example of such a structured level is the first quantum level (lvl QI.A) which tasks the player with inverting a sequence of single qubit gates. Of course, this problem would be trivial to those of you already familiar with quantum mechanics: you could use the linear algebra result (AB)^\dag = B^\dag A^\dag together with the knowledge that quantum gates are unitary, so the Hermitian conjugate of each gate doubles as its inverse. But what if you didn’t know quantum mechanics, or even linear algebra? Could this problem be solved through logical reasoning alone? This is where I think that the visuals really help; players should be able to infer several key points from geometry alone:

  • the inverse of a flip (or mirroring about some axis) is another equal flip.
  • the inverse of a rotation is an equal rotation in the opposite direction.
  • the last transformation done on each qubit should be the first transformation to be inverted.

So I think it is plausible that, even without prior knowledge in quantum mechanics or linear algebra, a player could not only solve the level but also grasp some important concepts (i.e. that quantum gates are invertible and that the order in which they are applied matters).

An early level challenges the player to invert the action of the 3 gates on the left. A solution is given on the right, formed by composing the inverse of each gate in reverse order.

Many of the levels in The Qubit Factory are also designed to be open-ended. Such levels, which often begin with a blank factory, have no single intended solution. The player is instead expected to use experimentation and creativity to design their own solution; this is the setting where I feel that the “game” format really shines. An example of an open-ended level is QIII.E, which gives the player 4 copies of a single qubit state \left| \psi \right\rangle, guaranteed to be either the +Z or +X eigenstate, and tasks the player to determine which state they have been given. Those familiar with quantum computing will recognize this as a relatively simple problem in state tomography. There are many viable strategies that could be employed to solve this task (and I am not even sure of the optimal one myself). However, by circumventing the need for a mathematical calculation, the Qubit Factory allows players to easily and quickly explore different approaches. Hopefully this could allow players to find effective strategies through trial-and-error, gaining some understanding of state tomography (and why it is challenging) in the process.

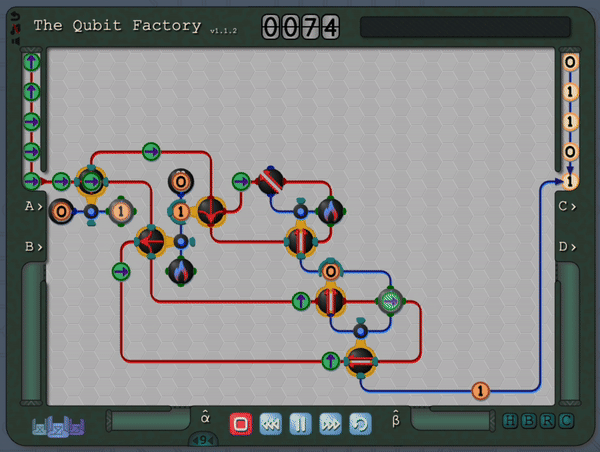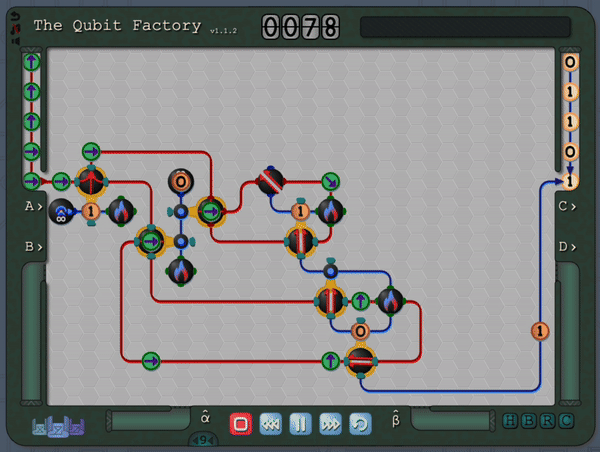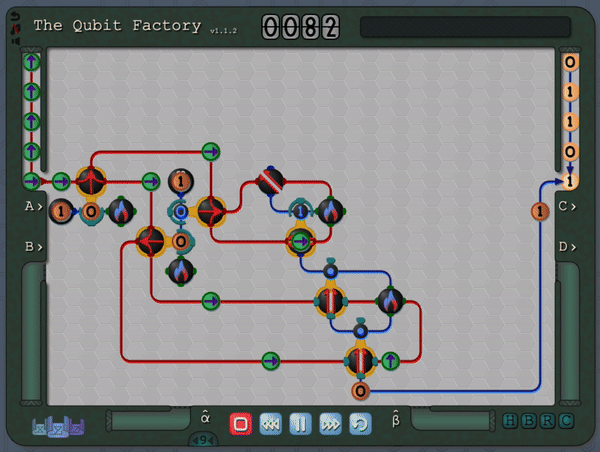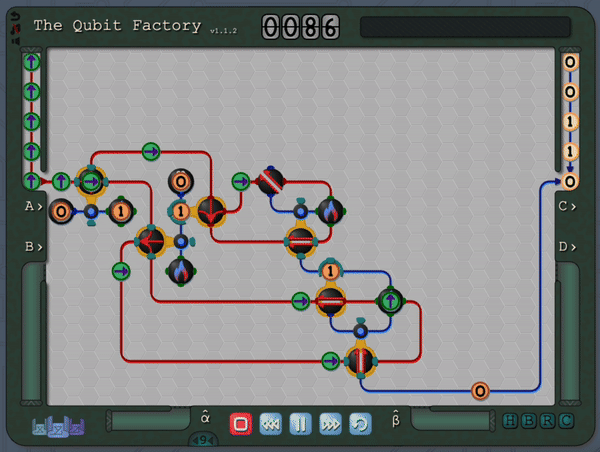
An example of a level in action! This level challenges the player to construct a circuit that can identify an unknown qubit state given several identical copies; a task in state tomography. The solution shown here uses a cascaded sequence of measurements, where the result of one measurement is used to control the axis of a subsequent measurement.

The Qubit Factory begins with levels covering the basics of qubits, gates and measurements. It later progresses to more advanced concepts like superpositions, basis changes and entangled states. Finally it culminates with levels based on introductory quantum protocols and algorithms (including quantum error correction, state tomography, super-dense coding, quantum repeaters, entanglement distillation and more). Even if you are familiar with the aforementioned material you should still be in for a substantial challenge, so please check it out if that sounds like your thing!

The Potential of Quantum Games

I believe that interactive games have great potential to provide new opportunities for people to better understand the quantum realm (a position shared by the IQIM, members of which have developed several projects in this area). As young children, playing is how we discover the world around us and build intuition for the rules that govern it. This is perhaps a significant reason why quantum mechanics is often a challenge for new students to learn; we don’t have direct experience or intuition with the quantum world in the same way that we do with the classical world. A quote from John Preskill puts it very succinctly:

“Perhaps kids who grow up playing quantum games will acquire a visceral understanding of quantum phenomena that our generation lacks.”

The Qubit Factory can be played at www.qubitfactory.io

You can win Tic Tac Toe, if you know quantum physics.

Posted on by
Reply

Note: Oliver Zheng is a senior at University High School, Irvine CA. He has been working on AI players for quantum versions of Tic Tac Toe under the supervision of Dr. Spiros Michalakis.

Several years ago, while scrolling through YouTube, I came across a video of Paul Rudd playing something called “Quantum Chess.” I had no idea what it was, nor did I know that it would become one of the most gloriously nerdy rabbit holes I would ever fall into (see: 5D Chess with Multiverse Time Travel).

Over time, I tried to teach myself how to play these multi-layered, multi-dimensional games, but progress was slow. However, while taking a break during a piano lesson last year, I mentioned to my teacher my growing interest in unnecessarily stressful versions of chess. She told me that she happened to be friends with Dr. Xie Chen, professor of theoretical physics at Caltech who was sponsoring a Quantum Gaming project. I immediately jumped at the opportunity to connect with her, and within days was able to have my first online meeting with Dr. Chen. Soon after, I got invited to join the project. Following my introduction to the team, I started reading “Quantum Computation and Quantum Information”, which helped me understand how the theory behind the games worked. When I felt ready, Dr. Chen referred me to Dr. Spiros Michalakis at Caltech, who, funnily enough, was the creator of the quantum chess video. 

I would’ve never imagined that I am two degrees of separation from Paul Rudd, but nonetheless, I wanted to share some of the work I’ve been doing with Spiros on Quantum TiqTaqToe.

What is Quantum TiqTaqToe?

Evert van Nieuwenburg, the creator of Quantum TiqTaqToe whom I also collaborated with, goes in depth about how the game works here, but I will give a short rundown. The general idea is that there is now a split move, where you can put an ‘X’ in two different squares at once — a Schrödinger’s X, if you will. When the board has no more empty squares, the X randomly ‘collapses’ into one of the two squares with equal probability. The game ends when there are three real X’s or three real O’s in a row, just as in regular tic-tac-toe. Depending on the mode you are playing, you might also be able to entangle your X’s with your opponent’s O’s. You can get a better sense of all this by actually playing the game here.

My goal was to find out who wins when both players play optimally. For instance, in normal tic-tac-toe, it is well-known that the first X should go in the middle of the board, and if player O counters successfully, the game should end in a tie. Is the outcome of Quantum TiqTaqToe, too, predetermined to end in a tie if both players play optimally? And, if not, what is the best first move for player X? I sought to answer these questions through the power of computation.

The First Attempt

In the following section, I refer to a ‘game state’ as any unique arrangement of X’s and O’s on a board. The ‘empty game state’ simply means an empty board. ‘Traversing’ through a certain game state means that, at some point in the game, that game state occurs. So, for example, every game traverses through the empty game state, since every game starts with an empty board.

In order to solve the unsolved, one must first solve the solved. As such, my first attempt was to create an algorithm that would figure out the best move to play in regular tic-tac-toe. This first attempt was rather straightforward, and I will explain it here:

Essentially, I developed a model using what is known as “reinforcement learning” to determine the best next move given a certain game state. Here is how it works: To track which set of moves are best for player X and player O, respectively, every game state is assigned a value, initially 0. When a game ends, these values are updated to reflect who won. The more games are played, the better these values reflect the sequence of moves that X and O must make to win or tie. To train this model (machine learning parlance for the algorithm that updates the values/parameters mentioned above), I programmed the computer to play randomly chosen moves for X and O, until the game ended. If, say, player X won, then the value of every game state traversed was increased by 1 to indicate that X was favored. On the other hand, if player O won, then the value of every game state traversed was decreased by 1 to indicate that O was favored. Here is an example:

X wins!

Let’s say that this is the first iteration that the model is trained on. Then, the next time the model sees this game state,

it will recognize that X has an advantage. In the same vein, the model now also thinks that the empty game state is favorable towards X, since, in the one game that was played, when the empty game state was traversed, X won.

If we run these randomized games enough times (I ran ten million iterations), every move in every game state has most likely been made, which means that the model is able to give a meaningful evaluation for any game state. However, there is one major problem with this approach, in that the model only indicates who is favored when they make a random move, not when they make the best move. To illustrate this, let’s examine the following game state:

(O’s turn)

Here, player O has two options: they can win the game by putting their O on the bottom center square, or lose the game by putting it on the right center square. Any seasoned tic-tac-toe player would make the right move in this scenario, and win the game. However, since the model trains on random moves, it thinks that player O will win half the time and lose half the time. Thus, to the model, this game state is not favorable to either player, when in reality it is absolutely favored towards O. 

During my first meeting with Spiros and Evert, they pointed out this flaw in my model. Evert suggested that I study up on something called a minimax algorithm, which circumvents this flaw, and apply it to tic-tac-toe. This set me on the next step of my journey.

Enter Minimax

The content of this section takes inspiration from this article.

In the minimax algorithm, the two players are known as the ‘maximizer’ and the ‘minimizer’. In the case of tic-tac-toe, X would be the maximizer and O the minimizer. The maximizer’s goal is to maximize their score, while the minimizer’s goal is to minimize their score. In tic-tac-toe, the minimax algorithm is implemented so that a win by X is a score of +1, a win by O is a score of -1, and a tie is simply 0. So X, seeking to maximize their score, would want to win, which makes sense.

Now, if X wanted to maximize their score through some move, they would have to consider O’s move, who would try to minimize the score. But before O makes their move, they would have to consider X’s next move. This creates a sort of back-and-forth, recursive dynamic in the minimax algorithm. In order for either player to make the best move, they would have to go through all possible moves they can make, and all possible moves their opponent can make after that, and so on and so forth. Here is a relatively simple example of the minimax algorithm at work:

Let’s start from the top. X has three possible moves they can make, and evaluates each of them. 

In the leftmost branch, the result is either -1 or 0, but which is the real score? Well, we expect O to make their best move, and since they are trying to minimize the score, we expect them to choose the ‘-1’ case. So we can say that this move results in a score of -1. 

In the middle branch, the result is either 1 or 0, and, following the same reasoning as before, O chooses the move corresponding to the minimal score, resulting in a score of 0.

Finally, the last branch results in X winning, so the score is +1.

Now, X can finally choose their best move, and in the interest of maximizing the score, places their X on the bottom right square. Intuitively, this makes sense because it was the only move that wins the game for X outright.

Great, but what would a minimax algorithm look like in Quantum Tiqtaqtoe?

Enter Expecti-Minimax

Expectiminimax contains the same core idea as minimax, but something interesting happens when the game board collapses. The algorithm can’t know for sure what the board will look like after collapse, so all it can do is calculate an expected value of the result (hence the name). Let’s look at an example:

Here, collapse occurs, and one branch (top) results in a tie, while the other (bottom) results in O winning. Since a tie is equal to 0 and an O win is equal to -1, the algorithm treats the score as

Note: the sum is divided by two because both outcomes have a ½ probability of occurring.

Solving the Game

Using the expecti-minimax algorithm, I effectively ‘solved’ the minimal and moderate versions of quantum tiqtaqtoe. However, even though the algorithm will always show the best move, the outcome from game to game might not be the same due to the inherent element of randomness. The most interesting of all my discoveries was probably the first move that the algorithm suggests for X, which I was able to make sense of both intuitively and logically. I challenge you all to find it! (Hint: it is the same for both the minimal and moderate versions.)

It turns out that when X plays optimally, they will always win the minimal version no matter what O plays. Meanwhile, in the moderate version, X will win most of the time, but not all the time. The probability distribution is as follows:

  (Another challenge: why are the denominators powers of two?)

Having satisfied my curiosity (for now), I’m looking forward to creating a new game of my own: 4 by 4 quantum tic-tac-toe. Currently, I am working on an algorithm that will give the best move, but since a 4×4 board is almost two times larger than a 3×3 board, the computational runtime of an expectiminimax algorithm would be far too large. As such, I am exploring the use of heuristics, which is sort of what the human mind uses to approach a game like tic-tac-toe. Because of this reliance on heuristics, there is no longer a guarantee that the algorithm will always make the best move, making this new adventure all the more mysterious and captivating.