Editor’s Note: Yesterday and today, Caltech is celebrating the inauguration of the Walter Burke Institute for Theoretical Physics. John Preskill made the following remarks at a dinner last night honoring the board of the Sherman Fairchild Foundation.
This is an exciting night for me and all of us at Caltech. Tonight we celebrate physics. Especially theoretical physics. And in particular the Walter Burke Institute for Theoretical Physics.
Some of our dinner guests are theoretical physicists. Why do we do what we do?
I don’t have to convince this crowd that physics has a profound impact on society. You all know that. We’re celebrating this year the 100th anniversary of general relativity, which transformed how we think about space and time. It may be less well known that two years later Einstein laid the foundations of laser science. Einstein was a genius for sure, but I don’t think he envisioned in 1917 that we would use his discoveries to play movies in our houses, or print documents, or repair our vision. Or see an awesome light show at Disneyland.
And where did this phone in my pocket come from? Well, the story of the integrated circuit is fascinating, prominently involving Sherman Fairchild, and other good friends of Caltech like Arnold Beckman and Gordon Moore. But when you dig a little deeper, at the heart of the story are two theorists, Bill Shockley and John Bardeen, with an exceptionally clear understanding of how electrons move through semiconductors. Which led to transistors, and integrated circuits, and this phone. And we all know it doesn’t stop here. When the computers take over the world, you’ll know who to blame.
Incidentally, while Shockley was a Caltech grad (BS class of 1932), John Bardeen, one of the great theoretical physicists of the 20th century, grew up in Wisconsin and studied physics and electrical engineering at the University of Wisconsin at Madison. I suppose that in the 1920s Wisconsin had no pressing need for physicists, but think of the return on the investment the state of Wisconsin made in the education of John Bardeen.
So, physics is a great investment, of incalculable value to society. But … that’s not why I do it. I suppose few physicists choose to do physics for that reason. So why do we do it? Yes, we like it, we’re good at it, but there is a stronger pull than just that. We honestly think there is no more engaging intellectual adventure than struggling to understand Nature at the deepest level. This requires attitude. Maybe you’ve heard that theoretical physicists have a reputation for arrogance. Okay, it’s true, we are arrogant, we have to be. But it is not that we overestimate our own prowess, our ability to understand the world. In fact, the opposite is often true. Physics works, it’s successful, and this often surprises us; we wind up being shocked again and again by “unreasonable effectiveness of mathematics in the natural sciences.” It’s hard to believe that the equations you write down on a piece of paper can really describe the world. But they do.
And to display my own arrogance, I’ll tell you more about myself. This occasion has given me cause to reflect on my own 30+ years on the Caltech faculty, and what I’ve learned about doing theoretical physics successfully. And I’ll tell you just three principles, which have been important for me, and may be relevant to the future of the Burke Institute. I’m not saying these are universal principles – we’re all different and we all contribute in different ways, but these are principles that have been important for me.
My first principle is: We learn by teaching.
Why do physics at universities, at institutions of higher learning? Well, not all great physics is done at universities. Excellent physics is done at industrial laboratories and at our national laboratories. But the great engine of discovery in the physical sciences is still our universities, and US universities like Caltech in particular. Granted, US preeminence in science is not what it once was — it is a great national asset to be cherished and protected — but world changing discoveries are still flowing from Caltech and other great universities.
Why? Well, when I contemplate my own career, I realize I could never have accomplished what I have as a research scientist if I were not also a teacher. And it’s not just because the students and postdocs have all the great ideas. No, it’s more interesting than that. Most of what I know about physics, most of what I really understand, I learned by teaching it to others. When I first came to Caltech 30 years ago I taught advanced elementary particle physics, and I’m still reaping the return from what I learned those first few years. Later I got interested in black holes, and most of what I know about that I learned by teaching general relativity at Caltech. And when I became interested in quantum computing, a really new subject for me, I learned all about it by teaching it.
Part of what makes teaching so valuable for the teacher is that we’re forced to simplify, to strip down a field of knowledge to what is really indispensable, a tremendously useful exercise. Feynman liked to say that if you really understand something you should be able to explain it in a lecture for the freshman. Okay, he meant the Caltech freshman. They’re smart, but they don’t know all the sophisticated tools we use in our everyday work. Whether you can explain the core idea without all the peripheral technical machinery is a great test of understanding.
And of course it’s not just the teachers, but also the students and the postdocs who benefit from the teaching. They learn things faster than we do and often we’re just providing some gentle steering; the effect is to amplify greatly what we could do on our own. All the more so when they leave Caltech and go elsewhere to change the world, as they so often do, like those who are returning tonight for this Symposium. We’re proud of you!
My second principle is: The two-trick pony has a leg up.
I’m a firm believer that advances are often made when different ideas collide and a synthesis occurs. I learned this early, when as a student I was fascinated by two topics in physics, elementary particles and cosmology. Nowadays everyone recognizes that particle physics and cosmology are closely related, because when the universe was very young it was also very hot, and particles were colliding at very high energies. But back in the 1970s, the connection was less widely appreciated. By knowing something about cosmology and about particle physics, by being a two-trick pony, I was able to think through what happens as the universe cools, which turned out to be my ticket to becoming a Caltech professor.
It takes a community to produce two-trick ponies. I learned cosmology from one set of colleagues and particle physics from another set of colleagues. I didn’t know either subject as well as the real experts. But I was a two-trick pony, so I had a leg up. I’ve tried to be a two-trick pony ever since.
Another great example of a two-trick pony is my Caltech colleague Alexei Kitaev. Alexei studied condensed matter physics, but he also became intensely interested in computer science, and learned all about that. Back in the 1990s, perhaps no one else in the world combined so deep an understanding of both condensed matter physics and computer science, and that led Alexei to many novel insights. Perhaps most remarkably, he connected ideas about error-correcting code, which protect information from damage, with ideas about novel quantum phases of matter, leading to radical new suggestions about how to operate a quantum computer using exotic particles we call anyons. These ideas had an invigorating impact on experimental physics and may someday have a transformative effect on technology. (We don’t know that yet; it’s still way too early to tell.) Alexei could produce an idea like that because he was a two-trick pony.
Which brings me to my third principle: Nature is subtle.
Yes, mathematics is unreasonably effective. Yes, we can succeed at formulating laws of Nature with amazing explanatory power. But it’s a struggle. Nature does not give up her secrets so readily. Things are often different than they seem on the surface, and we’re easily fooled. Nature is subtle.
Perhaps there is no greater illustration of Nature’s subtlety than what we call the holographic principle. This principle says that, in a sense, all the information that is stored in this room, or any room, is really encoded entirely and with perfect accuracy on the boundary of the room, on its walls, ceiling and floor. Things just don’t seem that way, and if we underestimate the subtlety of Nature we’ll conclude that it can’t possibly be true. But unless our current ideas about the quantum theory of gravity are on the wrong track, it really is true. It’s just that the holographic encoding of information on the boundary of the room is extremely complex and we don’t really understand in detail how to decode it. At least not yet.
This holographic principle, arguably the deepest idea about physics to emerge in my lifetime, is still mysterious. How can we make progress toward understanding it well enough to explain it to freshmen? Well, I think we need more two-trick ponies. Except maybe in this case we’ll need ponies who can do three tricks or even more. Explaining how spacetime might emerge from some more fundamental notion is one of the hardest problems we face in physics, and it’s not going to yield easily. We’ll need to combine ideas from gravitational physics, information science, and condensed matter physics to make real progress, and maybe completely new ideas as well. Some of our former Sherman Fairchild Prize Fellows are leading the way at bringing these ideas together, people like Guifre Vidal, who is here tonight, and Patrick Hayden, who very much wanted to be here. We’re very proud of what they and others have accomplished.
Bringing ideas together is what the Walter Burke Institute for Theoretical Physics is all about. I’m not talking about only the holographic principle, which is just one example, but all the great challenges of theoretical physics, which will require ingenuity and synthesis of great ideas if we hope to make real progress. We need a community of people coming from different backgrounds, with enough intellectual common ground to produce a new generation of two-trick ponies.
Finally, it seems to me that an occasion as important as the inauguration of the Burke Institute should be celebrated in verse. And so …
Who studies spacetime stress and strain
And excitations on a brane,
Where particles go back in time,
And physicists engage in rhyme?
Whose speedy code blows up a star
(Though it won’t quite blow up so far),
Where anyons, which braid and roam
Annihilate when they get home?
Who makes math and physics blend
Inside black holes where time may end?
Where do they do all this work?
The Institute of Walter Burke!
We’re very grateful to the Burke family and to the Sherman Fairchild Foundation. And we’re confident that your generosity will make great things happen!
“. Imagine turning on a magnetic field, or coupling one electron to another, or letting the superconductor sit untouched. A CPTP map, labeled as
, represents every such evolution.
. If your measurement device (your photodetector, spectrometer, etc.) worked perfectly, you’d read out one of several possible numbers. Let
denote the probability that you read out the
possible number. Because your device outputs some number, the probabilities sum to one:
. We say that
“has trace one.” But you don’t measure
; you switch on the magnetic field.
undergoes the process
, becoming a quantum state
. Imagine that, after the process ended, you measured a property of
. If your measurement device worked perfectly, you’d read out one of several possible numbers. Let
denote the probability that you read out the
possible number. The probabilities sum to one:
.
“has trace one”, so the map
is “trace preserving”.
are positive (actually, nonnegative) because they lie between zero and one. Since the
characterize a crucial aspect of
, we call
“positive” (though we should call
“nonnegative”).
turns the positive
into the positive
. Since
maps positive objects to positive objects, we call
“positive”.
also satisfies a stronger condition, so we call such maps “completely positive.”**
.
 and that
and that ![]() is defined on
is defined on 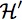 . “
. “![]() is positive” means
is positive” means 
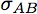 defined on a Hilbert space
defined on a Hilbert space 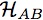 .
. ![]() acts on the system’s part of state. Let
acts on the system’s part of state. Let  denote the identity operation that maps every possible environment state to itself. Suppose that
denote the identity operation that maps every possible environment state to itself. Suppose that ![]() changes the system’s state while
changes the system’s state while  preserves the environment’s state. The system-and-environment composite ends up in the state
preserves the environment’s state. The system-and-environment composite ends up in the state  . This state is positive, so we call
. This state is positive, so we call ![]() “completely positive”:
“completely positive”:


