Monthly Archives: July 2017

The sign problem(s)

Posted on by
2

The thirteen-month-old had mastered the word “dada” by the time I met her. Her parents were teaching her to communicate other concepts through sign language. Picture her, dark-haired and bibbed, in a high chair. Banana and mango slices litter the tray in front of her. More fruit litters the floor in front of the tray. The baby lifts her arms and flaps her hands.

Dada looks up from scrubbing the floor.

“Look,” he calls to Mummy, “she’s using sign language! All done.” He performs the gesture that his daughter seems to have aped: He raises his hands and rotates his forearms about his ulnas, axes perpendicular to the floor. “All done!”

The baby looks down, seizes another morsel, and stuffs it into her mouth.

“Never mind,” Dada amends. “You’re not done, are you?”

His daughter had a sign(-language) problem.

Banana

So does Dada, MIT professor Aram Harrow. Aram studies quantum information theory. His interests range from complexity to matrices, from resource theories to entropies. He’s blogged for The Quantum Pontiff, and he studies—including with IQIM postdoc Elizabeth Crosson—the quantum sign problem.

Imagine calculating properties of a chunk of fermionic quantum matter. The chunk consists of sites, each inhabited by one particle or by none. Translate as “no site can house more than one particle” the jargon “the particles are fermions.”

The chunk can have certain amounts of energy. Each amount E_j corresponds to some particle configuration indexed by j: If the system has some amount E_1 of energy, particles occupy certain sites and might not occupy others. If the system has a different amount E_2 \neq E_1 of energy, particles occupy different sites. A Hamiltonian, a mathematical object denoted by H, encodes the energies E_j and the configurations. We represent H with a matrix, a square grid of numbers.

Suppose that the chunk has a temperature T = \frac{ 1 }{ k_{\rm B} \beta }. We could calculate the system’s heat capacity, the energy required to raise the chunk’s temperature by one Kelvin. We could calculate the free energy, how much work the chunk could perform in powering a motor or lifting a weight. To calculate those properties, we calculate the system’s partition function, Z.

How? We would list the configurations j. With each configuration, we would associate the weight e^{ - \beta E_j }. We would sum the weights: Z = e^{ - \beta E_1 }  +  e^{ - \beta E_2}  +  \ldots  =  \sum_j e^{ - \beta E_j}.

Easier—like feeding a 13-month-old—said than done. Let N denote the number of qubits in the chunk. If N is large, the number of configurations is gigantic. Our computers can’t process so many configurations. This inability underlies quantum computing’s promise of speeding up certain calculations.

We don’t have quantum computers, and we can’t calculate Z. Can we  approximate Z?

Yes, if H “lacks the sign problem.” The math that models our system models also a classical system. If our system has D dimensions, the classical system has D+1 dimensions. Suppose, for example, that our sites form a line. The classical system forms a square.

We replace the weights e^{ - \beta E_j } with different weights—numbers formed from a matrix that represents H. If H lacks the sign problem, the new weights are nonnegative and behave like probabilities. Many mathematical tools suit probabilities. Aram and Elizabeth apply such tools to Z, here and here, as do many other researchers.

We call Hamiltonians that lack the sign problem “stoquastic,” which I think fanquastic.1 Stay tuned for a blog post about stoquasticity by Elizabeth.

What if H has the sign problem? The new weights can assume negative and nonreal values. The weights behave unlike probabilities; we can’t apply those tools. We find ourselves knee-deep in banana and mango chunks.

Mango chunks

Solutions to the sign problem remain elusive. Theorists keep trying to mitigate the problem, though. Aram, Elizabeth, and others are improving calculations of properties of sign-problem-free systems. One scientist-in-the-making has achieved a breakthrough: Aram’s daughter now rotates her hands upon finishing meals and when she wants to leave her car seat or stroller.

One sign problem down; one to go.

Mess

With gratitude to Aram’s family for its hospitality and to Elizabeth Crosson for sharing her expertise.

1For experts: A local Hamiltonian is stoquastic relative to the computational basis if each local term is represented, relative to the computational basis, by a matrix whose off-diagonal entries are real and nonpositive.

Entropy Avengers

Posted on by
1

As you already know if you read my rare (but highly refined!) blog samples, I have spent a big chunk of my professorial career teaching statistical mechanics. And if you teach statistical mechanics, there is pretty much one thing you obsess about: entropy.

So you can imagine my joy of finally seeing a fully anti-entropic superhero appearing on my facebook account (physics enthusiasts out there – the project is seeking support on Kickstarter):

Apart from the plug for Assa Auerbach’s project (which, for full disclosure, I have just supported), I would like to use this as an excuse to share my lessons about entropy. With the same level of seriousness. Here they are, in order of increasing entropy.

1. Cost of entropy. Entropy is always marketed as a very palpable thing. Disorder. In class, however, it is calculated via an enumeration of the ‘microscopic states of the system’. For an atomic gas I know how to calculate the entropy (throw me at the blackboard in the middle of the night, no problem. Bosons or Fermions – anytime!) But how can the concept be applied to our practical existence? I have a proposal:

Quantify entropy by the cost (in $’s) of cleaning up the mess!

Examples can be found at all scales. For anything household-related, we should use the H_k constant. H_k=$25/hour for my housekeeper. You break a glass – it takes about 10 minutes to clean. That puts the entropy of the wreckage at $4.17. Having a birthday party takes about 2 hours to clean up: $50 entropy.

Another insight which my combined experience as professor and parent has produced:

2. Conjecture: Babies are maximally efficient topological entropy machines. If you raised a 1 year-old you know exactly what I mean. You can at least guess why maximum efficiency. But why topological? A baby sauntering through the house leaves a string of destruction behind itself. The baby is a mess-creation string-operator! If you start lagging behind, doom will emerge – hence the maximum efficiency. By the way, the only strategy viable is to undo the damage as it happens. But this blog post is about entropy, not about parenting.

In fact, this allows us to establish a conversion of entropy measured in k_B units, to its, clearly more natural, measure in dollar units. A baby eats about 1000kCal/day=4200kJ/day. To fully deal with the consequences, we need a housekeeper to visit about once a week. 4200kJ/day times 7 days=29400 kJoules. These are consumed at T=300K. So an entropy of S=Q/T~100J/K, which is also S~6 \times 10^{24} (Q/k_B T) in dimensionless units, converts to S~$120, which is the cost of our weekly housekeeper visit. This gives a value of $ 10^{-23} per entropy of a two-level system. Quite a reasonable bang for the buck, don’t you think?

3. My conjecture (2) fails. The second law of thermodynamics is an inequality. Entropy \geq Q/T. Why does the conjecture fail? Babies are not ‘maximal’. Consider presidents. Consider the mess that the government can make. It is at the scale of trillions per year. $ 10^{12}. Using the rigorous conversion rule established above, this corresponds to 10^{35} two-level systems. Which happens to quite precisely match the combined number of electrons present in the human bodies of all our military personnel. But the mess, however, is created by very few individuals.

Given the large amounts of taxpayer money we dish out to deal with entropy in the world, Auerbach’s book is bound to make a big impact. In fact, maybe Max the demon would one day be nominated for the national medal of freedom, or at least be inducted into the National Academy of Sciences.

The world of hackers and secrets

Posted on by
16

I’m Evgeny Mozgunov, and some of you may remember my earlier posts on Quantum Frontiers. I’ve recently graduated with a PhD after 6 years in the quantum information group at Caltech. As I’m navigating the job market in quantum physics, it was only a matter of time before I got dragged into a race between startups. Those who can promise impressive quantum speedups for practical tasks get a lot of money from venture capitalists. Maybe there’s something about my mind and getting paid: when I’m paid to do something, I suddenly start coming up with solutions that never occurred to me while I was wandering around as a student. And this time, I’ve noticed a possibility of impressing the public with quantum speedups that nobody has ever used before.

Three former members of John Preskill’s group, Gorjan Alagic, Stacey Jeffery and Stephen Jordan, have already proposed this idea (Circuit Obfuscation Using Braids, p.10), but none of the startups seems to have picked it up. You only need a small quantum computer. Imagine you are in the audience. I ask you to come up with a number. Don’t tell it out loud: instead, write it on a secret piece of paper, and take a little time to do a few mathematical operations based on the number. Then announce the result of those operations. Once you are done, people will automatically be split into two categories. Those with access to a small quantum computer (like the one at IBM) will be able to put on a magic hat (the computer…) and recover your number. But the rest of the audience will be left in awe, with no clue as to how this is even possible. There’s nothing they could do to guess your number based only on the result you announced, unless you’re willing to wait for a few days and they have access to the world’s supercomputing powers.

So far I’ve described the general setting of encryption – a cipher is announced, the key to the cipher is destroyed, and only those who can break the code can decipher.  For instance, if RSA encryption is used for the magic show above, indeed only people with a big quantum computer will be able to recover the secret number. To complete my story, I need to describe what the result that you announce (the cipher) looks like:

A sequence of instructions for a small quantum computer that is equivalent to a simple instruction for spitting out your number. However, the announced sequence of instructions is obfuscated, such that you can’t just read off the number from it.

You really need to feed the sequence into a quantum computer, and see what it outputs. Obfuscation is more general than encryption, but here we’re going to use it as a method of encryption.

Alagic et al. taught us how to do something called obfuscation by compiling for a quantum computer: much like when you compile a .c file in your CS class, you can’t really understand the .out file. Of course you can just execute the .out file, but not if it describes a quantum circuit, unless you have access to a quantum computer. 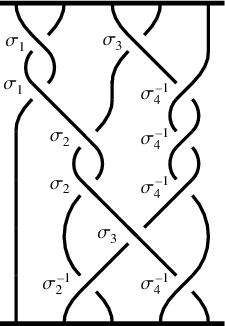The proposed classical compiler turns either a classical or a quantum algorithm into a hard-to-read quantum circuit that looks like braidsBraid_1000.gif. Unfortunately, any obfuscation by compiling scheme has the problem that whoever understands the compiler well enough will be able to actually read the .out file (or notice a pattern in braids reduced to a compact “normal” form), and guess your number without resorting to a quantum computer. Surprisingly, even though Alagic et al.’s scheme doesn’t claim any protection under this attack, it still satisfies one of the theoretical definitions of obfuscation: if two people write two different sets of instructions to perform the same operation, and then each obfuscate their own set of instructions by a restricted set of tricks, then it should be impossible to tell from the end result which program was obtained by whom.

forQF2.jpg

Theoretical obfuscation can be illustrated by these video game Nier cosplayers: when they put on their wig and blindfold, they look like the same person. The character named 2B is an android, whose body is disposable, and whose mind is a set of instructions stored on a server. Other characters try to hack her mind as the story progresses.

Quantum scientists can have their own little world of hackers and secrets, organized in the following way: some researchers present their obfuscated code outputting a secret message, and other researchers become hackers trying to break it. Thanks to another result by Alagic et al, we know that hard-to-break obfuscated circuits secure against classical computers exist. But we don’t know how the obfuscator that produces those worst-case instances reliably looks like, so a bit of crowdsourcing to find it is in order. It’s a free-for-all, where all tools and tricks are allowed. In fact, even you can enter! All you need to know is a universal gate set H,T = R(π/4),CNOT and good old matrix multiplication. Come up with a product of these matrices that multiplies to a bunch of X‘s (X=HT⁴H), but such that only you know on which qubits the X are applied. This code will spit out your secret bitstring on an input of all 0’es. Publish it and wait until some hacker breaks it!

Here’s mine, can anyone see what’s my secret bitstring?

Obfuscated circuit.png

One can run it on a 5 qubit quantum computer in less than 1ms. But if you try to multiply the corresponding 32×32 matrices on your laptop, it takes more than 1ms. Quantum speedup right there. Of course I didn’t prove that there’s no better way of finding out my secret than multiplying matrices. In fact, had I used only even powers of the matrix T in the picture above, then there is a classical algorithm available in open source (Aaronson, Gottesman) that recovers the number without having to multiply large matrices.

I’m in luck: startups and venture capitalists never cared about theoretical proofs, it only has to work until it fails. I think they should give millions to me instead of D-wave. Seriously, there’s plenty of applications for practical obfuscation, besides magic shows. One can set up a social network where posts are gibberish except for those who have a quantum computer (that would be a good conspiracy theory some years from now). One can verify when a private company claims to sell a small quantum computer.

I’d like to end on a more general note: small quantum computers are already faster than classical hardware at multiplying certain kinds of matrices. This has already been proven for a restricted class of quantum computers and a task called boson sampling. If there’s a competition in matrix multiplication somewhere in the world, we can already win.