Hamiltonian: An American Musical (without Americana or music)

Author’s note: I intended to post this article three months ago. Other developments delayed the release. Thanks in advance for pardoning the untimeliness.

Critics are raving about it. Barak Obama gave a speech about it. It’s propelled two books onto bestseller lists. Committees have showered more awards on it than clouds have showered rain on California this past decade.

What is it? The Hamiltonian, represented by $\hat{H}$ . It’s an operator (a mathematical object) that basically represents a system’s energy. Hamiltonians characterize systems classical and quantum, from a brick in a Broadway theater to the photons that form a spotlight. $\hat{H}$ determines how a system evolves, or changes in time.

I lied: Obama didn’t give a speech about the Hamiltonian. He gave a speech about Hamilton. Hamilton: An American Musical spotlights 18th-century revolutionary Alexander Hamilton. Hamilton conceived the United States’s national bank. He nurtured the economy as our first Secretary of the Treasury. The year after Alexander Hamilton died, William Rowan Hamilton was born. Rowan Hamilton conceived four-dimensional numbers called quaternions. He nurtured the style of physics, Hamiltonian mechanics, used to model quantum systems today.

Hamilton has enchanted audiences and critics. Ticket sell out despite costing over $1,000. Tonys, Grammys, and Pulitzers have piled up. Lawmakers, one newspaper reported, ridicule colleagues who haven’t seen the show. One political staff member confessed that “dodging ‘Hamilton’ barbs has affected her work—so much so that she hasn’t returned certain phone calls ‘because I couldn’t handle the anxiety’ of being harangued for her continued failure to see the show.”

Musical-theater fans across the country are applauding Alexander. Hamilton forbid that William Rowan should envy him. Let’s celebrate Hamiltonians.

I’ve been pondering the Hamiltonian

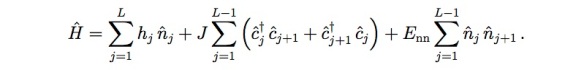
It describes a chain of $L$ sites. $L$ ranges from 10 to 30 in most computer simulations. The cast consists of quantum particles. Each site houses one particle or none. $\hat{n}_j$ represents the number of particles at site $j$ . $c_j$ represents the removal of a particle from site $j$ , and $c_j^\dag$ represents the adding of a particle.

The last term in $\hat{H}$ represents the repulsion between particles that border each other. The “nn” in “ $E_{\rm nn}$ ” stands for “nearest-neighbor.” The $J$ term encodes particles’ hopping between sites. $\hat{c}_j^\dag \hat{c}_{j+1}$ means, “A particle jumps from site $j+1$ to site $j$ .”

The first term in $\hat{H}$ , we call disorder. Imagine a landscape of random dips and hills. Imagine, for instance, crouching on the dirt and snow in Valley Forge. Boots and hooves have scuffed the ground. Zoom in; crouch lower. Imagine transplanting the row of sites into this landscape. $h_j$ denotes the height of site $j$ .

Say that the dips sink low and the hills rise high. The disorder traps particles like soldiers behind enemy lines. Particles have trouble hopping. We call this system many-body localized.

Imagine flattening the landscape abruptly, as by stamping on the snow. This flattening triggers a phase transition. Phase transitions are drastic changes, as from colony to country. The flattening frees particles to hop from site to site. The particles spread out, in accordance with the Hamiltonian’s $J$ term. The particles come to obey thermodynamics, a branch of physics that I’ve effused about.

The Hamiltonian encodes repulsion, hopping, localization, thermalization, and more behaviors. A richer biography you’ll not find amongst the Founding Fathers.

As Hamiltonians constrain particles, politics constrain humans. A play has primed politicians to smile upon the name “Hamilton.” Physicists study Hamiltonians and petition politicians for funding. Would politicians fund us more if we emphasized the Hamiltonians in our science?

Gold star for whoever composes the most rousing lyrics about many-body localization. Or, rather, fifty white stars.