Like many mathematically inclined teenagers, I was charmed when I first read the book Flatland by Edwin Abbott Abbott.* It’s a story about a Sphere who visits a two-dimensional world and tries to awaken its inhabitants to the existence of a third dimension. As perceived by Flatlanders, the Sphere is a circle which appears as a point, grows to maximum size, then shrinks and disappears.

My memories of Flatland were aroused as I read a delightful recent paper by Max Metlitski, Charlie Kane, and Matthew Fisher about magnetic monopoles and three-dimensional bosonic topological insulators. To explain why, I’ll need to recall a few elements of the theory of monopoles and of topological insulators, before returning to the connection between the two and why that reminds me of Flatland.

Flatlanders, confined to the two-dimensional surface of a topological insulator, are convinced by a magnetic monopole that a third dimension must exist.

Monopoles

Paul Dirac was no ordinary genius. Aside from formulating relativistic electron theory and predicting the existence of antimatter, Dirac launched the quantum theory of magnetic monopoles in a famous 1931 paper. Dirac envisioned a magnetic monopole as a semi-infinitely long, infinitesimally thin string of magnetic flux, such that the end of the string, where the flux spills out, seems to be a magnetic charge. For this picture to make sense, the string should be invisible. Dirac pointed out that an electron with electric charge e, transported around a string carrying flux 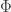, could detect the string (via what later came to be called the Aharonov-Bohm effect) unless the flux is an integer multiple of 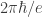, where 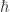is Planck’s constant. Conversely, in order for the string to be invisible, if a magnetic monopole exists with magnetic charge , then all electric charges must be integer multiples of e. Thus the existence of magnetic monopoles (which have never been observed) could explain quantization of electric charge (which has been observed).

Captivated by the beauty of his own proposal, Dirac concluded his paper by remarking, “One would be surprised if Nature had made no use of it.”

Our understanding of quantized magnetic monopoles advanced again in 1979 when another extraordinary physicist, Edward Witten, discussed a generalization of Dirac’s quantization condition. Witten noted that the Lagrange density of electrodynamics could contain a term of the form

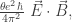
where 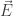is the electric field and is the magnetic field. This “ term” may also be expressed as

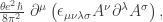
where A is the vector potential, and hence is a total derivative which makes no contribution to the classical field equations of electrodynamics. But Witten realized that it can have important consequences for the quantum properties of magnetic monopoles. Specifically, the term modifies the field momentum conjugate to the vector potential, which becomes

Because the Gauss law condition satisfied by physical quantum states is altered, for a monopole with magnetic charge 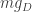, where is Dirac’s minimal charge 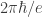and m is an integer, the allowed values of the electric charge become

where n is an integer. This spectrum of allowed charges remains invariant if advances by 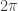, suggesting that the parameter is actually an angular variable with period 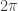. This periodicity of can be readily verified in a theory admitting fermions with the minimal charge e. But if the charged particles are bosons then turns out to be a periodic variable with period 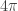instead.

That has a different period for a bosonic theory than a fermionic one has an interesting interpretation. As Goldhaber noticed in 1976, dyons carrying both magnetic and electric charge can exhibit statistical transmutation. That is, in a purely bosonic theory, a dyon with magnetic charge and electric charge ne is a fermion if n is an odd integer — when two dyons are exchanged, transport of each dyon’s electric charge in the magnetic field of the other dyon induces a sign change in the wave function. In a fermionic theory the story is different; now we can think of the dyon as a fermionic electric charge bound to a bosonic monopole. There are two canceling contributions to the exchange phase of the dyon, which is therefore a boson for any integer value of n, whether even or odd.

As smoothly increases from 0 to 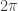, the statistics (whether bosonic or fermionic) of a dyon remains fixed even as the dyon’s electric charge increases by e. For the bosonic theory with 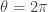, then, dyons with magnetic charge and electric charge ne are bosons for n odd and fermions for n even, the opposite of what happens when 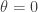. For the bosonic theory, unlike the fermionic theory, we need to increase by 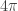for the physics of dyons to be fully invariant.

In 1979 Ed Witten was a postdoc at Harvard, where I was a student, though he was visiting CERN for the summer when he wrote his paper about the -dependent monopole charge. I always read Ed’s papers carefully, but I gave special scrutiny to this one because magnetic monopoles were a pet interest of mine. At the time, I wondered whether the Witten effect might clarify how to realize the parameter in a lattice gauge theory. But it certainly did not occur to me that the -dependent electric charge of a magnetic monopole could have important implications for quantum condensed matter physics. Theoretical breakthroughs often have unexpected consequences, which may take decades to emerge.

Symmetry-protected topological phases

Okay, now let’s talk about topological insulators, a very hot topic in condensed matter physics these days. Actually, a topological insulator is a particular instance of a more general concept called a symmetry-protected topological phase of matter (or SPT phase). Consider a d-dimensional hunk of material with a (d-1)-dimensional boundary. If the material is in an SPT phase, then the physics of the d-dimensional bulk is boring — it’s just an insulator with an energy gap, admitting no low-energy propagating excitations. But the physics of the (d-1)-dimensional edge is exotic and exciting — for example the edge might support “gapless” excitations of arbitrarily low energy which can conduct electricity. The exotica exhibited by the edge is a consequence of a symmetry, and is destroyed if the symmetry is broken either explicitly or spontaneously; that is why we say the phase is “symmetry protected.”

The low-energy edge excitations can be described by a (d-1)-dimensional effective field theory. But for a typical SPT phase, this effective field theory is what we call anomalous, which means that for one reason or another the theory does not really make sense. The anomaly tells us something interesting and important, namely that the (d-1)-dimensional theory cannot be really, truly (d-1) dimensional; it can arise only at the edge of a higher-dimensional system.

This phenomenon, in which the edge does not make sense by itself without the bulk, is nicely illustrated by the integer quantum Hall effect, which occurs in a two-dimensional electron system in a high magnetic field and at low temperature, if the sample is sufficiently clean so that the electrons are highly mobile and rarely scattered by impurities. In this case the relevant symmetry is electron number, or equivalently the electric charge. At the one-dimensional edge of a two-dimensional quantum Hall sample, charge carriers move in only one direction — to the right, say, but not to the left. A theory with such chiral electric charges does not really make sense. One problem is that electric charge is not conserved — an electric field along the edge causes charge to be locally created, which makes the theory inconsistent.

The way the theory resolves this conundrum is quite remarkable. A two-dimensional strip of quantum Hall fluid has two edges, one at the top, the other at the bottom. While the top edge has only right-moving excitations, the bottom edge has only left-moving excitations. When electric charge appears on the top edge, it is simultaneously removed from the bottom edge. Rather miraculously, charge can be conveyed across the bulk from one edge to the other, even though the bulk does not have any low-energy excitations at all.

I first learned about this interplay of edge and bulk physics from a beautiful 1985 paper by Curt Callan and Jeff Harvey. They explained very lucidly how an edge theory with an anomaly and a bulk theory with an anomaly can fit together, with each solving the other’s problems. Curiously, the authors did not mention any connection with the quantum Hall effect, which had been discovered five years earlier, and I didn’t appreciate the connection myself until years later.

Topological insulators

In the case of topological insulators, the symmetries which protect the gapless edge excitations are time-reversal invariance and conserved particle number, i.e. U(1) symmetry. Though the particle number might not be coupled to an electromagnetic gauge field, it is instructive for the purpose of understanding the properties of the symmetry-protected phase to imagine that the U(1) symmetry is gauged, and then to consider the potential anomalies that could afflict this gauge symmetry. The first topological insulators conceived by theorists were envisioned as systems of non-interacting electrons whose properties were relatively easy to understand using band theory. But it was not so clear at first how interactions among the electrons might alter their exotic behavior. The wonderful thing about anomalies is that they are robust with respect to interactions. In many cases we can infer the features of anomalies by studying a theory of non-interacting particles, assured that these features survive even when the particles interact.

As have many previous authors, Metlitski et al. argue that when we couple the conserved particle number to a U(1) gauge field, the effective theory describing the bulk physics of a topological insulator in three dimensions may contain a term. But wait … since the electric field is even under time reversal and the magnetic field is odd, the term is T-odd; under T, is mapped to 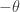, so T seems to be violated if has any nonzero value. Except … we have to remember that is really a periodic variable. For a fermionic topological insulator the period is 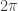; therefore the theory with 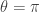is time reversal invariant; 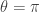maps to under T, which is equivalent to a rotation of by 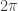. For a bosonic topological insulator the period is 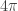, which means that 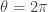is the nontrivial T-invariant value.

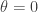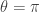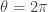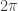If we say that a “trivial” insulator (e.g., the vacuum) has , then we may say that a bulk material with (fermionic case) or (bosonic case) is a “nontrivial” (a.k.a. topological) insulator. At the edge of the sample, where bulk material meets vacuum, must rotate suddenly by (fermions) or by (bosons). The exotic edge physics is a consequence of this abrupt change in .

Monopoles in Flatland

To understand the edge physics, and in particular to grasp how fermionic and bosonic topological insulators differ, Metlitski et al. invite us to imagine a magnetic monopole with magnetic charge passing through the boundary between the bulk and the surrounding vacuum. To the Flatlanders confined to the surface of the bulk sample, the passing monopole induces a sudden change in the magnetic flux through the surface by a single flux quantum , which could arise due to a quantum tunneling event. What does the Flatlander see?

In a fermionic topological insulator, there is a monopole that carries charge e/2 when inside the sample (where ) and charge 0 when outside (where 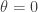). Since electric charge is surely conserved in the full three-dimensional theory, the change in the monopole’s charge must be compensated by a corresponding change in the charge residing on the surface. Flatlanders are puzzled to witness a spontaneously arising excitation with charge e/2. This is an anomaly — electric charge conservation is violated, which can only make sense if Flatlanders are confined to a surface in a higher-dimensional world. Though unable to escape their surface world, the Flatlanders can be convinced by the Monopole that an extra dimension must exist.

In a bosonic topological insulator, the story is somewhat different: there is a monopole that carries electric charge 0 when inside the sample (where ) and charge –e when outside (where 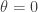). In this case, though, there are bosonic charge-e particles living on the surface. A monopole can pick up a charged particle as it passes through Flatland, so that its charge is 0 both inside the bulk sample and outside in the vacuum. Flatlanders are happy — electric charge is conserved!

But hold on … there’s still something wrong. Inside the bulk (where ) a monopole with electric charge 0 is a fermion, while outside in the vacuum (where 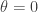) it is a boson. In the three-dimensional theory it is not possible for any local process to create an isolated fermion, so if the fermionic monopole becomes a bosonic monople as it passes through Flatland, it must leave a fermion behind. Flatlanders are puzzled to witness a spontaneously arising fermion. This is an anomaly — conservation of fermionic parity is violated, which can only make sense if Flatlanders are confined to a surface in a higher-dimensional world. Once again, the clever residents of Flatland learn from the Monopole about an extra spatial dimension, without ever venturing outside their two-dimensional home.

Topological order gets edgy

This post is already pretty long and I should wrap it up. Before concluding I’ll remark that the theory of symmetry-protected phases has been developing rapidly in recent months.

In particular, a new idea, introduced last fall by Vishwanath and Senthil, has been attracting increasing attention. While in most previously studied SPT phases the unbroken symmetry protects gapless excitations confined to the edge of the sample, Vishwanath and Senthil pointed out another possibility — a gapped edge exhibiting topological order. The surface can support anyons with exotic braiding statistics.

Here, too, anomalies are central to the discussion. While anyons in two-dimensional media are already a much-studied subject, the anyon models that can be realized at the edges of three-dimensional SPT phases are different than anyon models realized in really, truly two-dimensional systems. What’s new are not the braiding properties of the anyons, but rather how the anyons transform under the symmetry. Flatlanders who study the symmetry realization in their gapped two-dimensional world should be able to infer the existence of the three-dimensional bulk.

The pace of discovery picked up this month when four papers appeared simultaneously on the preprint arXiv, by Metlitski-Kane-Fisher, Chen-Fidkowski-Vishwanath, Bonderson-Nayak-Qi, and Wang-Potter-Senthil, all proposing and analyzing models of SPT phases with gapped edges. It remains to be seen, though, whether this physics will be realized in actual materials.

Are we on the edge?

In Flatland, our two-dimensional friend, finally able to perceive the third dimension thanks to the Sphere’s insistent tutelage, begs to enter a world of still higher dimensions, “where thine own intestines, and those of kindred Spheres, will lie exposed to … view.” The Sphere is baffled by the Flatlander’s request, protesting, “There is no such land. The very idea of it is utterly inconceivable.”

Let’s not be so dogmatic as the Sphere. The lessons learned from the quantum Hall effect and the topological insulator have prepared us to take the next step, envisioning our own three-dimensional world as the edge of a higher-dimensional bulk system. The existence of an unseen bulk may be inferred in the future by us edgelings, if experimental explorations of our three-dimensional effective theory reveal anomalies begging for an explanation.

Perhaps we are on the edge … of a great discovery. At least it’s conceivable.

*Disclaimer: The gender politics of Flatland, to put it mildly, is outdated and offensive. I don’t wish to endorse the idea that women are one dimensional! I included the reference to Flatland because the imagery of two-dimensional beings struggling to imagine the third dimension is a perfect fit to the scientific content of this post.