On last week’s “Welcome to the math olympics”, I closed with a problem from the International Math Olympiad of 1981 (a bad year for wine – I would know, I was an avid drinker back then). I would like to take some time to present a solution to this problem, because this is where all the magic happens. What magic? You will see. Here is the problem again:
Problem 6 (IMO 1981, modified): If 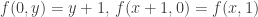 and
and  , for all non-negative integers
, for all non-negative integers  , find
, find 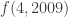 .
.
The solution that follows uses solely elementary mathematics. What does that mean? It means that a 15 year-old can figure out the solution, given enough time and an IQ of 300. And, indeed, there are some who can solve this problem in 15 minutes. But, as you will see, it takes clarity of mind that is only attained through relentless effort. Effort to the outside world – to you, it will feel like you are going down the rabbit-hole and you don’t want the journey to end. But you must enter this world with wonder, because it is the world of the imagination – a world where your greatest weapon is your curiosity, prodding your mind to see how far the rabbit-hole goes.
Continue reading →
, such that



