Monthly Archives: January 2024

“Once Upon a Time”…with a twist

Posted on by
5
The Noncommuting-Charges World Tour (Part 1 of 4)

This is the first part in a four part series covering the recent Perspectives article on noncommuting charges. I’ll be posting one part every ~6 weeks leading up to my PhD thesis defence.

Thermodynamics problems have surprisingly many similarities with fairy tales. For example, most of them begin with a familiar opening. In thermodynamics, the phrase “Consider an isolated box of particles” serves a similar purpose to “Once upon a time” in fairy tales—both serve as a gateway to their respective worlds. Additionally, both have been around for a long time. Thermodynamics emerged in the Victorian era to help us understand steam engines, while Beauty and the Beast and Rumpelstiltskin, for example, originated about 4000 years ago. Moreover, each conclude with important lessons. In thermodynamics, we learn hard truths such as the futility of defying the second law, while fairy tales often impart morals like the risks of accepting apples from strangers. The parallels go on; both feature archetypal characters—such as wise old men and fairy godmothers versus ideal gases and perfect insulators—and simplified models of complex ideas, like portraying clear moral dichotomies in narratives versus assuming non-interacting particles in scientific models.1

Of all the ways thermodynamic problems are like fairytale, one is most relevant to me: both have experienced modern reimagining. Sometimes, all you need is a little twist to liven things up. In thermodynamics, noncommuting conserved quantities, or charges, have added a twist.

Unfortunately, my favourite fairy tale, ‘The Hunchback of Notre-Dame,’ does not start with the classic opening line ‘Once upon a time.’ For a story that begins with this traditional phrase, ‘Cinderella’ is a great choice.

First, let me recap some of my favourite thermodynamic stories before I highlight the role that the noncommuting-charge twist plays. The first is the inevitability of the thermal state. For example, this means that, at most times, the state of most sufficiently small subsystem within the box will be close to a specific form (the thermal state).

The second is an apparent paradox that arises in quantum thermodynamics: How do the reversible processes inherent in quantum dynamics lead to irreversible phenomena such as thermalization? If you’ve been keeping up with Nicole Yunger Halpern‘s (my PhD co-advisor and fellow fan of fairytale) recent posts on the eigenstate thermalization hypothesis (ETH) (part 1 and part 2) you already know the answer. The expectation value of a quantum observable is often comprised of a sum of basis states with various phases. As time passes, these phases tend to experience destructive interference, leading to a stable expectation value over a longer period. This stable value tends to align with that of a thermal state’s. Thus, despite the apparent paradox, stationary dynamics in quantum systems are commonplace.

The third story is about how concentrations of one quantity can cause flows in another. Imagine a box of charged particles that’s initially outside of equilibrium such that there exists gradients in particle concentration and temperature across the box. The temperature gradient will cause a flow of heat (Fourier’s law) and charged particles (Seebeck effect) and the particle-concentration gradient will cause the same—a flow of particles (Fick’s law) and heat (Peltier effect). These movements are encompassed within Onsager’s theory of transport dynamics…if the gradients are very small. If you’re reading this post on your computer, the Peltier effect is likely at work for you right now by cooling your computer.

What do various derivations of the thermal state’s forms, the eigenstate thermalization hypothesis (ETH), and the Onsager coefficients have in common? Each concept is founded on the assumption that the system we’re studying contains charges that commute with each other (e.g. particle number, energy, and electric charge). It’s only recently that physicists have acknowledged that this assumption was even present.

This is important to note because not all charges commute. In fact, the noncommutation of charges leads to fundamental quantum phenomena, such as the Einstein–Podolsky–Rosen (EPR) paradox, uncertainty relations, and disturbances during measurement. This raises an intriguing question. How would the above mentioned stories change if we introduce the following twist?

“Consider an isolated box with charges that do not commute with one another.” 

This question is at the core of a burgeoning subfield that intersects quantum information, thermodynamics, and many-body physics. I had the pleasure of co-authoring a recent perspective article in Nature Reviews Physics that centres on this topic. Collaborating with me in this endeavour were three members of Nicole’s group: the avid mountain climber, Billy Braasch; the powerlifter, Aleksander Lasek; and Twesh Upadhyaya, known for his prowess in street basketball. Completing our authorship team were Nicole herself and Amir Kalev.

To give you a touchstone, let me present a simple example of a system with noncommuting charges. Imagine a chain of qubits, where each qubit interacts with its nearest and next-nearest neighbours, such as in the image below.

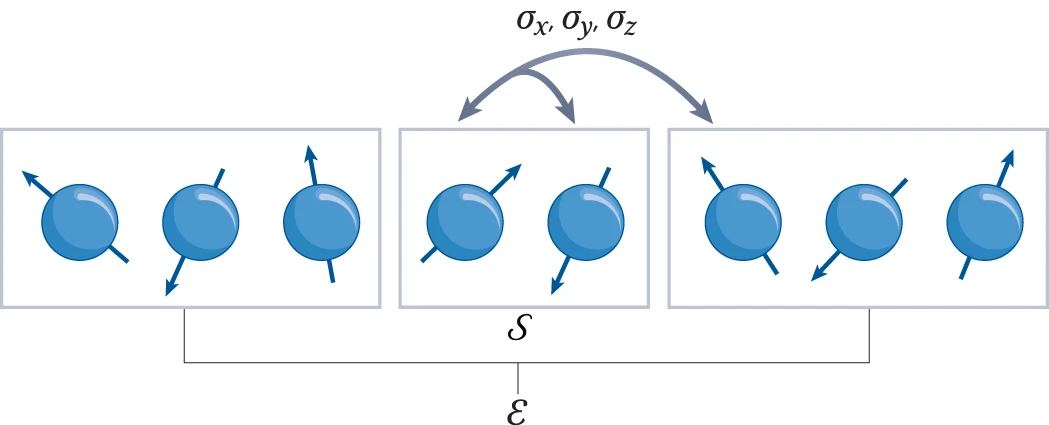
The figure is courtesy of the talented team at Nature. Two qubits form the system S of interest, and the rest form the environment E. A qubit’s three spin components, σa=x,y,z, form the local noncommuting charges. The dynamics locally transport and globally conserve the charges.

In this interaction, the qubits exchange quanta of spin angular momentum, forming what is known as a Heisenberg spin chain. This chain is characterized by three charges which are the total spin components in the x, y, and z directions, which I’ll refer to as Qx, Qy, and Qz, respectively. The Hamiltonian H conserves these charges, satisfying [H, Qa] = 0 for each a, and these three charges are non-commuting, [Qa, Qb] ≠ 0, for any pair a, b ∈ {x,y,z} where a≠b. It’s noteworthy that Hamiltonians can be constructed to transport various other kinds of noncommuting charges. I have discussed the procedure to do so in more detail here (to summarize that post: it essentially involves constructing a Koi pond).

This is the first in a series of blog posts where I will highlight key elements discussed in the perspective article. Motivated by requests from peers for a streamlined introduction to the subject, I’ve designed this series specifically for a target audience: graduate students in physics. Additionally, I’m gearing up to defending my PhD thesis on noncommuting-charge physics next semester and these blog posts will double as a fun way to prepare for that.

  1. This opening text was taken from the draft of my thesis. ↩︎

Colliding the familiar and the anti-familiar at CERN

Posted on by
1

The most ingenious invention to surprise me at CERN was a box of chocolates. CERN is a multinational particle-physics collaboration. Based in Geneva, CERN is famous for having “the world’s largest and most powerful accelerator,” according to its website. So a physicist will take for granted its colossal magnets, subatomic finesse, and petabytes of experimental data. 

But I wasn’t expecting the chocolates.

In the main cafeteria, beside the cash registers, stood stacks of Toblerone. Sweet-tooth owners worldwide recognize the yellow triangular prisms stamped with Toblerone’s red logo. But I’d never seen such a prism emblazoned with CERN’s name. Scientists visit CERN from across the globe, and probably many return with Swiss-chocolate souvenirs. What better way to promulgate CERN’s influence than by coupling Switzerland’s scientific might with its culinary?1

I visited CERN last November for Sparks!, an annual public-outreach event. The evening’s speakers and performers offer perspectives on a scientific topic relevant to CERN. This year’s event highlighted quantum technologies. Physicist Sofia Vallecorsa described CERN’s Quantum Technology Initiative, and IBM philosopher Mira Wolf-Bauwens discussed ethical implications of quantum technologies. (Yes, you read that correctly: “IBM philosopher.”) Dancers Wenchi Su and I-Fang Lin presented an audiovisual performance, Rachel Maze elucidated government policies, and I spoke about quantum steampunk. 

Around Sparks!, I played the physicist tourist: presented an academic talk, descended to an underground detector site, and shot the scientific breeze with members of the Quantum Technology Initiative. (What, don’t you present academic talks while touristing?) I’d never visited CERN before, but much of it felt eerily familiar. 

A theoretical-physics student studies particle physics and quantum field theory (the mathematical framework behind particle physics) en route to a PhD. CERN scientists accelerate particles to high speeds, smash them together, and analyze the resulting debris. The higher the particles’ initial energies, the smaller the debris’s components, and the more elementary the physics we can infer. CERN made international headlines in 2012 for observing evidence of the Higgs boson, the particle that endows other particles with masses. As a scientist noted during my visit, one can infer CERN’s impact from how even Auto World (if I recall correctly) covered the Higgs discovery. Friends of mine process data generated by CERN, and faculty I met at Caltech helped design CERN experiments. When I mentioned to a colleague that I’d be flying to Geneva, they responded, “Oh, are you visiting CERN?” All told, a physicist can avoid CERN as easily as one can avoid the Panama Canal en route from the Atlantic Ocean to the Pacific through South America. So, although I’d never visited, CERN felt almost like a former stomping ground. It was the details that surprised me.

Familiar book, new (CERN) bookstore.

Take the underground caverns. CERN experiments take place deep underground, where too few cosmic rays reach to muck with observations much. I visited the LHCb experiment, which spotlights a particle called the “beauty quark” in Europe and the less complimentary “bottom quark” in the US. LHCb is the first experiment that I learned has its own X/Twitter account. Colloquia (weekly departmental talks at my universities) had prepared me for the 100-meter descent underground, for the hard hats we’d have to wear, and for the detector many times larger than I.

A photo of the type bandied about in particle-physics classes
A less famous hard-hat photo, showing a retired detector’s size.

But I hadn’t anticipated the bright, single-tone colors. Between the hard hats and experimental components, I felt as though I were inside the Google logo.

Or take CERN’s campus. I wandered around it for a while before a feeling of nostalgia brought me up short: I was feeling lost in precisely the same way in which I’d felt lost countless times at MIT. Numbers, rather than names, label both MIT’s and CERN’s buildings. Somebody must have chosen which number goes where by throwing darts at a map while blindfolded. Part of CERN’s hostel, building 39, neighbors buildings 222 and 577. I shouldn’t wonder to discover, someday, that the CERN building I’m searching for has wandered off to MIT.

Part of the CERN map. Can you explain it?

Between the buildings wend streets named after famous particle physicists. I nodded greetings to Einstein, Maxwell, Democritus (or Démocrite, as the French Swiss write), and Coulomb. But I hadn’t anticipated how much civil engineers venerate particle physicists. So many physicists did CERN’s designers stuff into walkways that the campus ran out of streets and had to recycle them. Route W. F. Weisskopf turns into Route R. P. Feynman at a…well, at nothing notable—not a fork or even a spoon. I applaud the enthusiasm for history; CERN just achieves feats in navigability that even MIT hasn’t.

The familiar mingled with the unfamiliar even in the crowd on campus. I was expecting to recognize only the personnel I’d coordinated with electronically. But three faces surprised me at my academic talk. I’d met those three physicists through different channels—a summer school in Malta, Harvard collaborators, and the University of Maryland—at different times over the years. But they happened to be visiting CERN at the same time as I, despite their not participating in Sparks! I’m half-reminded of the book Roughing It, which describes how Mark Twain traveled the American West via stagecoach during the 1860s. He ran into a long-lost friend “on top of the Rocky Mountains thousands of miles from home.” Exchange “on top of the Rockies” for “near the Alps” and “thousands of miles” for “even more thousands of miles.”

CERN unites physicists. We learn about its discoveries in classes, we collaborate on its research or have friends who do, we see pictures of its detectors in colloquia, and we link to its science-communication pages in blog posts. We respect CERN, and I hope we can be forgiven for fondly poking a little fun at it. So successfully has CERN spread its influence, I felt a sense of recognition upon arriving. 

I didn’t buy any CERN Toblerones. But I arrived home with 4.5 pounds of other chocolates, which I distributed to family and friends, the thermodynamics lunch group I run at the University of Maryland, and—perhaps most importantly—my research group. I’ll take a leaf out of CERN’s book: to hook students on fundamental physics, start early, and don’t stint on the sweets.

With thanks to Claudia Marcelloni, Alberto Di Meglio, Michael Doser, Antonella Del Rosso, Anastasiia Lazuka, Salome Rohr, Lydia Piper, and Paulina Birtwistle for inviting me to, and hosting me at, CERN.

1After returning home, I learned that an external company runs CERN’s cafeterias and that the company orders and sells the Toblerones. Still, the idea is brilliant.