Monthly Archives: July 2016

Quantum Supremacy: The US gets serious

Posted on by
9

If you have been paying any attention to the news on quantum computing and the evolution of industrial and national efforts towards realizing a scalable, fault-tolerant quantum computer that can tackle problems intractable to current supercomputing capabilities, then you know that something big is stirring throughout the quantum world.

More than 15 years ago, Microsoft decided to jump into the quantum computing business betting big on topological quantum computing as the next big thing. The new website of Microsoft’s Station Q shows that keeping a low profile is no longer an option. This is a sentiment that Google clearly shared, when back in 2013, they decided to promote their new partnership with NASA Ames and D-Wave, known as the Quantum A.I. Lab, through a YouTube video that went viral (disclosure: they do own Youtube.) In fact, IQIM worked with Google at the time to get kids excited about the quantum world by developing qCraft, a mod introducing quantum physics into the world of Minecraft. Then, a few months ago, IBM unveiled the quantum experience website, which captured the public’s imagination by offering a do-it-yourself opportunity to run an algorithm on a 5-qubit quantum chip in the cloud.

But, looking at the opportunities for investment in academic groups working on quantum computing, companies like Microsoft were/are investing heavily in experimental labs across the pond, such as Leo Kowenhoven’s group at TU Delft and Charlie Marcus’ group in Copenhagen, with smaller investments here in the US. This may just reflect the fact that the best efforts to build topological qubits are in Europe, but it still begs the question why a fantastic idea like topologically protected majorana zero modes, by Yale University’s Nick Read and Dmitry Green, which inspired the now famous Majorana wire paper by Alexei Kitaev when he was a researcher at Microsoft’s Redmond research lab, and whose transition from theory to experiment took off with contributions from Maryland and IQIM researchers, was outsourced to European labs for experimental verification and further development. The one example of a large investment in a US academic research group has been Google’s hiring of John Martinis away from UCSB. In fact, John and I met a couple of years ago to discuss investment into his superconducting quantum computing efforts, because government funding for academic efforts to actually build a quantum computer was lacking. China was investing, Canada was investing, Europe went a little crazy, but the US was relying on visionary agencies like IARPA, DARPA and the NSF to foot the bill (without which Physics Frontiers Centers like IQIM wouldn’t be around). In short, there was no top-down policy directive to focus national attention and inter-agency Federal funding on winning the quantum supremacy race.

Until now.

The National Science and Technology Council, which is chaired by the President of the United States and “is the principal means within the executive branch to coordinate science and technology policy across the diverse entities that make up the Federal research and development enterprise”, just released the following report:

Advancing Quantum Information Science: National Challenges and Opportunities

The White House blog post does a good job at describing the high-level view of what the report is about and what the policy recommendations are. There is mention of quantum sensors and metrology, of the promise of quantum computing to material science and basic science, and they even go into the exciting connections between quantum error-correcting codes and emergent spacetime, by IQIM’s Pastawski, et al.

But the big news is that the report recommends significant and sustained investment in Quantum Information Science. The blog post reports that the administration intends “to engage academia, industry, and government in the upcoming months to … exchange views on key needs and opportunities, and consider how to maintain vibrant and robust national ecosystems for QIS research and development and for high-performance computing.”

Personally, I am excited to see how the fierce competition at the academic, industrial and now international level will lead to a race for quantum supremacy. The rivals are all worthy of respect, especially because they are vying for supremacy not just over each other, but over a problem so big and so interesting, that anyone’s success is everyone’s success. After all, anyone can quantum, and if things go according to plan, we will soon have the first generation of kids trained on hourofquantum.com (it doesn’t exist yet), as well as hourofcode.com. Until then, quantum chess and qCraft will have to do.

Bringing the heat to Cal State LA

Posted on by
8

John Baez is a tough act to follow.

The mathematical physicist presented a colloquium at Cal State LA this May.1 The talk’s title: “My Favorite Number.” The advertisement image: A purple “24” superimposed atop two egg cartons.

Baez300px

The colloquium concerned string theory. String theorists attempt to reconcile Einstein’s general relativity with quantum mechanics. Relativity concerns the large and the fast, like the sun and light. Quantum mechanics concerns the small, like atoms. Relativity and with quantum mechanics individually suggest that space-time consists of four dimensions: up-down, left-right, forward-backward, and time. String theory suggests that space-time has more than four dimensions. Counting dimensions leads theorists to John Baez’s favorite number.

His topic struck me as bold, simple, and deep. As an otherworldly window onto the pedestrian. John Baez became, when I saw the colloquium ad, a hero of mine.

And a tough act to follow.

I presented Cal State LA’s physics colloquium the week after John Baez. My title: “Quantum steampunk: Quantum information applied to thermodynamics.” Steampunk is a literary, artistic, and film genre. Stories take place during the 1800s—the Victorian era; the Industrial era; an age of soot, grime, innovation, and adventure. Into the 1800s, steampunkers transplant modern and beyond-modern technologies: automata, airships, time machines, etc. Example steampunk works include Will Smith’s 1999 film Wild Wild West. Steampunk weds the new with the old.

So does quantum information applied to thermodynamics. Thermodynamics budded off from the Industrial Revolution: The steam engine crowned industrial technology. Thinkers wondered how efficiently engines could run. Thinkers continue to wonder. But the steam engine no longer crowns technology; quantum physics (with other discoveries) does. Quantum information scientists study the roles of information, measurement, and correlations in heat, energy, entropy, and time. We wed the new with the old.

Posters

What image could encapsulate my talk? I couldn’t lean on egg cartons. I proposed a steampunk warrior—cravatted, begoggled, and spouting electricity. The proposal met with a polite cough of an email. Not all department members, Milan Mijic pointed out, had heard of steampunk.

Steampunk warrior

Milan is a Cal State LA professor and my erstwhile host. We toured the palm-speckled campus around colloquium time. What, he asked, can quantum information contribute to thermodynamics?

Heat offers an example. Imagine a classical (nonquantum) system of particles. The particles carry kinetic energy, or energy of motion: They jiggle. Particles that bump into each other can exchange energy. We call that energy heat. Heat vexes engineers, breaking transistors and lowering engines’ efficiencies.

Like heat, work consists of energy. Work has more “orderliness” than the heat transferred by random jiggles. Examples of work exertion include the compression of a gas: A piston forces the particles to move in one direction, in concert. Consider, as another example, driving electrons around a circuit with an electric field. The field forces the electrons to move in the same direction. Work and heat account for all the changes in a system’s energy. So states the First Law of Thermodynamics.

Suppose that the system is quantum. It doesn’t necessarily have a well-defined energy. But we can stick the system in an electric field, and the system can exchange motional-type energy with other systems. How should we define “work” and “heat”?

Quantum information offers insights, such as via entropies. Entropies quantify how “mixed” or “disordered” states are. Disorder grows as heat suffuses a system. Entropies help us extend the First Law to quantum theory.

First slide

So I explained during the colloquium. Rarely have I relished engaging with an audience as much as I relished engaging with Cal State LA’s. Attendees made eye contact, posed questions, commented after the talk, and wrote notes. A student in a corner appeared to be writing homework solutions. But a presenter couldn’t have asked for more from the rest. One exclamation arrested me like a coin in the cogs of a grandfather clock.

I’d peppered my slides with steampunk art: paintings, drawings, stills from movies. The peppering had staved off boredom as I’d created the talk. I hoped that the peppering would stave off my audience’s boredom. I apologized about the trimmings.

“No!” cried a woman near the front. “It’s lovely!”

I was about to discuss experiments by Jukka Pekola’s group. Pekola’s group probes quantum thermodynamics using electronic circuits. The group measures heat by counting the electrons that hop from one part of the circuit to another. Single-electron transistors track tunneling (quantum movements) of single particles.

Heat complicates engineering, calculations, and California living. Heat scrambles signals, breaks devices, and lowers efficiencies. Quantum heat can evade definition. Thermodynamicists grind their teeth over heat.

“No!” the woman near the front had cried. “It’s lovely!”

She was referring to steampunk art. But her exclamation applied to my subject. Heat has not only practical importance, but also fundamental: Heat influences every law of thermodynamics. Thermodynamic law underpins much of physics as 24 underpins much of string theory. Lovely, I thought, indeed.

Cal State LA offered a new view of my subfield, an otherworldly window onto the pedestrian. The more pedestrian an idea—the more often the idea surfaces, the more of our world the idea accounts for—the deeper the physics. Heat seems as pedestrian as a Pokémon Go player. But maybe, someday, I’ll present an idea as simple, bold, and deep as the number 24.

Window

A window onto Cal State LA.

With gratitude to Milan Mijic, and to Cal State LA’s Department of Physics and Astronomy, for their hospitality.

1For nonacademics: A typical physics department hosts several presentations per week. A seminar relates research that the speaker has undertaken. The audience consists of department members who specialize in the speaker’s subfield. A department’s astrophysicists might host a Monday seminar; its quantum theorists, a Wednesday seminar; etc. One colloquium happens per week. Listeners gather from across the department. The speaker introduces a subfield, like the correction of errors made by quantum computers. Course lectures target students. Endowed lectures, often named after donors, target researchers.

The physics of Trump?? Election renormalization.

Image

12

Two things were high in my mind this last quarter: My course on advanced statistical mechanics and phase transitions, and the bizarre general elections that raged all around. It is no wonder then, that I would start to conflate the Ising model, Landau mean field, and renormalization group, with the election process, and just think of each and every one of us as a tiny magnet, that needs to say up or down – Trump or Cruz, Clinton or Sanders (a more appetizing choice, somehow), and .. you get the drift.

Elections and magnetic phase transitions are very much alike. The latter, I will argue, teaches us something very important about the former.

The physics of magnetic phase transitions is amazing. If I hadn’t thought this way, I wouldn’t be a condensed matter physicist. Models of magnets consider a bunch of spins – each one a small magnet – that talk only to their nearest neighbor, as happens in typical magnets. At the onset of magnetic order (the Curie temperature), when the symmetry of the spins becomes broken, it turns out that the spin correlation length diverges. Even though Interaction length = lattice constant, we get correlation length = infinity.

To understand how ridiculous this is, you should understand what a correlation length is. The correlation tells you a simple thing. If you are a spin, trying to make it out in life, and trying to figure out where to point, your pals around you are certainly going to influence you. Their pals will influence them, and therefore you. The correlation length tells you how distant can a spin be, and still manage to nudge you to point up or down. In physics-speak, it is the reduced correlation length. It makes sense that somebody in you neighborhood, or your office, or even your town, will do something that will affect you – after all – you always interact with people that distant. But the analogy to the spins is that there is always a given circumstance where some random person in Incheon, South Korea, could influence your vote. A diverging correlation length is the Butterfly effect for real.

And yet, spins do this. At the critical temperature, just as the spins decide whether they want to point along the north pole or towards Venus, every nonsense of a fluctuation that one of them makes leagues away may galvanize things one way or another. Without ever even remotely directly talking to even their father’s brother’s nephew’s cousin’s former roommate! Every fluctuation, no matter where, factors into the symmetry breaking process.

A bit of physics, before I’m blamed for being crude in my interpretation. The correlation length at the Curie point, and almost all symmetry-breaking continuous transitions, diverges as some inverse power of the temperature difference to the critical point: \frac{1}{|T-T_c|}^{\nu}. The faster it diverges (the higher the power \nu) , actually the more feeble the symmetry breaking is. Why is that? After I argued that this is an amazing phenomenon? Well, if 10^2 voices can shift you one way or another, each voice is worth something. 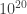If 10^{20} voices are able to push you around, I’m not really buying influence on you by bribing ten of these. Each voice is worth less. Why? The correlation length is also a measure of the uncertainty before the moment of truth – when the battle starts and we don’t know who wins. Big correlation length – any little element of the battlefield can change something, and many souls are involved and active. Small correlation length – the battle was already decided since one of the sides has a single bomb that will evaporate the world. Who knew that Dr. Strangelove could be a condensed matter physicist?

This lore of correlations led to one of the most breathtaking developments of 20th century physics. I’m a condensed matter guy, so it is natural that Ken Wilson, as well as Ben Widom, Michael Fisher, and Leo Kadanoff are my superheros. They came up with an idea so simple yet profound – scaling. If you have a system (say, of spins) that you can’t figure out – maybe because it is fluctuating, and because it is interacting – regardless, all you need to do is to move away from it. Let averaging (aka, central limit theorem) do the job and suppress fluctuations. Let us just zoom out. If we change the scale by a factor of 2, so that all spins look more crowded, then the correlation length also look half as big. The system looks less critical. It is as if we managed to move away from the critical temperature – either cooling towards 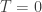T=0 , or heating up towards T=\infty. Both limits are easy to solve. How do we make this into a framework? If the pre-zoom-out volume had 8 spins, we can average them into a representative single spin. This way you’ll end up with a system that looks pretty much like the one you had before – same spin density, same interaction, same physics – but at a different temperature, and further from the phase transition. It turns out you can do this, and you can figure out how much changed in the process. Together, this tells you how the correlation length depends on T-T_c. This is the renormalization group, aka, RG.

Interestingly, this RG procedure informs us that criticality and symmetry breaking are more feeble the lower the dimension. There are no 1d permanent magnets, and magnetism in 2d is very frail. Why? Well, the more dimensions there are, the more nearest neighbors each spin has, and more neighbors your neighbors have. Think about the 6-degrees of separation game. 3d is okay for magnets, as we know. It turns out, however, that in physical systems above 4 dimensions, critical phenomena is the same as that of a fully connected (infinite dimensional) network. The uncertainty stage is very small, correlations length diverge slowly. Even at distance 1 there are enough people or spins to bend your will one way or another. Magnetization is just a question of time elapsed from the beginning of the experiment.

Spins, votes, what’s the difference? You won’t be surprised to find that the term renormalization has permeated every aspect of economics and social science as well. What is voting Republican vs Democrat if not a symmetry breaking? Well, it is not that bad yet – the parties are different. No real symmetry there, you would think. Unless you ask the ‘undecided voter’.

And if elections are affected by such correlated dynamics, what about revolutions? Here the analogy with phase transitions is so much more prevalent even in our language – resistance to a regime solidifies, crystallizes, and aligns – just like solids and magnets. When people are fed up with a regime, the crucial question is – if I would go to the streets, will I be joined by enough people to affect a change?

Revolutions, therefore, seem to rise out of strong fluctuations in the populace. If you wish, think of revolutions as domains where the frustration is so high, which give a political movement the inertia it needs.

Domains-: that’s exactly what the correlation length is about. The correlation length is the size of correlated magnetic domains, i.e.,groups of spins that point in the same direction. And now we remember that close to a phase transition, the correlation length diverges as some power of the distance ot the transition: \frac{1}{|T-T_c|^{\nu}}. Take a magnet just above its Curie temperature. The closer we are to a phase transition, the larger the correlation length is, and the bigger are the fluctuating magnetized domains. The parameter \nu is the correlation-length critical exponent and something of a holy grail for practitioners of statistical mechanics. Everyone wants to calculate it for various phase transition. It is not that easy. That’s partially why I have a job.

The correlation length aside, how many spins are involved in a domain? \left[1/|T-T_c|^d\right]^{\nu} . Actually, we know roughly what \nu is. For systems with dimension $latex  d>4$, it is ½. For systems with a lower dimensionality it is roughly $latex  2/d$. (Comment for the experts: I’m really not kidding – this fits the Ising model for 2 and 3 dimensions, and it fits the xy model for 3d).

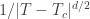So the number of spins in a domain in systems below 4d is 1/|T-T_c|^2, independent of dimension. On the other hand, four d and up it is 1/|T-T_c|^{d/2}. Increasing rapidly with dimension, when we are close to the critical point.

Back to voters. In a climate of undecided elections, analogous to a magnet near its Curie point, the spins are the voters, and domain walls are the crowds supporting this candidate or that policy; domain walls are what becomes large demonstrations in the Washington Mall. And you would think that the world we live in is clearly 2d – a surface of a 3d sphere (and yes – that includes Manhattan!). So a political domain size just diverges as a simple moderate 1/|T-T_c|^2 during times of contested elections.

Something happened, however, in the past two decades: the internet. The connectivity of the world has changed dramatically.

No more 2d. Now, our effective dimension is determined by our web based social network. Facebook perhaps? Roughly speaking, the dimensionality of the Facebook network is that number of friends we have, divided by the number of mutual friends. I venture to say this averages at about 10. With about a 150 friends in tow, out of which 15 are mutual. So our world, for election purposes, is 10 dimensional big!

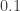Let’s simulate what this means for our political system. Any event – a terrorist attack, or a recession, etc. will cause a fluctuation that will involve a large group of people – a domain. Take a time when T-T_c is a healthy 0.1 for instance. In the good old 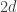2d world this would involve 100 friends times 1/0.1^2\sim 10000 people. Now it would be more like 100\cdot 1/0.1^{10/2}\sim 10-millions. So any small perturbation of conditions could make entire states turn one way or another.

When response to slight shifts in prevailing conditions encompasses entire states, rather than entire neighborhoods, polarization follows. Over all, a state where each neighborhood has a slightly different opinion will be rather moderate – extreme opinions will only resonate locally. Single voices could only sway so many people. But nowadays, well – we’ve all seen Trump and the like on the march. Millions. It’s not even their fault – its physics!

Can we do anything about it? It’s up for debate. Maybe cancel the electoral college, to make the selecting unit larger than the typical size of a fluctuating domain. Maybe carry out a time averaged election: make an election year where each month there is a contest for the grand prize. Or maybe just move to Canada.