My maternal grandfather gave me an antique key when I was in middle school. I loved the workmanship: The handle consisted of intertwined loops. I loved the key’s gold color and how the key weighed on my palm. Even more, I loved the thought that the key opened something. I accompanied my mother to antique shops, where I tried unlocking chests, boxes, and drawers.

My grandfather’s antique key
I found myself holding another such key, metaphorically, during the autumn of 2018. MIT’s string theorists had requested a seminar, so I presented about quasiprobabilities. Quasiprobabilities represent quantum states similarly to how probabilities represent a swarm of classical particles. Consider the steam rising from asphalt on a summer day. Calculating every steam particle’s position and momentum would require too much computation for you or me to perform. But we can predict the probability that, if we measure every particle’s position and momentum, we’ll obtain such-and-such outcomes. Probabilities are real numbers between zero and one. Quasiprobabilities can assume negative and nonreal values. We call these values “nonclassical,” because they’re verboten to the probabilities that describe classical systems, such as steam. I’d defined a quasiprobability, with collaborators, to describe quantum chaos.

David Arvidsson-Shukur was sitting in the audience. David is a postdoctoral fellow at the University of Cambridge and a visiting scholar in the other Cambridge (at MIT). He has a Swedish-and-southern-English accent that I’ve heard only once before and, I learned over the next two years, an academic intensity matched by his kindliness.1 Also, David has a name even longer than mine: David Roland Miran Arvidsson-Shukur. We didn’t know then, but we were destined to journey together, as postdoctoral knights-errant, on a quest for quantum truth.
David studies the foundations of quantum theory: What distinguishes quantum theory from classical? David suspected that a variation on my quasiprobability could unlock a problem in metrology, the study of measurements.

Suppose that you’ve built a quantum computer. It consists of gates—uses of, e.g., magnets or lasers to implement logical operations. A classical gate implements operations such as “add 11.” A quantum gate can implement an operation that involves some number more general than 11. You can try to build your gate correctly, but it might effect the wrong
value. You need to measure
.
How? You prepare some quantum state and operate on it with the gate.
imprints itself on the state, which becomes
. Measure some observable
. You repeat this protocol in each of many trials. The measurement yields different outcomes in different trials, according to quantum theory. The average amount of information that you learn about
per trial is called the Fisher information.

Let’s change this protocol. After operating with the gate, measure another observable, , and postselect: If the
measurement yields a desirable outcome
, measure
. If the
-measurement doesn’t yield the desirable outcome, abort the trial, and begin again. If you choose
and
adroitly, you’ll measure
only when the trial will provide oodles of information about
. You’ll save yourself many
measurements that would have benefited you little.2

Why does postselection help us? We could understand easily if the system were classical: The postselection would effectively improve the input state. To illustrate, let’s suppose that (i) a magnetic field implemented the gate and (ii) the input were metal or rubber. The magnetic field wouldn’t affect the rubber; measuring in rubber trials would provide no information about the field. So you could spare yourself
measurements by postselecting on the system’s consisting of metal.
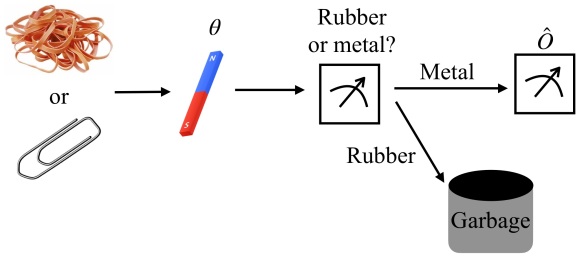
Postselection on a quantum system can defy this explanation. Consider optimizing your input state , beginning each trial with the quantum equivalent of metal. Postselection could still increase the average amount of information information provided about
per trial. Postselection can enhance quantum metrology even when postselection can’t enhance the classical analogue.
David suspected that he could prove this result, using, as a mathematical tool, the quasiprobability that collaborators and I had defined. We fulfilled his prediction, with Hugo Lepage, Aleks Lasek, Seth Lloyd, and Crispin Barnes. Nature Communications published our paper last month. The work bridges the foundations of quantum theory with quantum metrology and quantum information theory—and, through that quasiprobability, string theory. David’s and my quantum quest continues, so keep an eye out for more theory from us, as well as a photonic experiment based on our first paper.

I still have my grandfather’s antique key. I never found a drawer, chest, or box that it opened. But I don’t mind. I have other mysteries to help unlock.
1The morning after my wedding this June, my husband and I found a bouquet ordered by David on our doorstep.
2Postselection has a catch: The measurement has a tiny probability of yielding the desirable outcome. But, sometimes, measuring
costs more than preparing
, performing the gate, and postselecting. For example, suppose that the system is a photon. A photodetector will measure
. Some photodetectors have a dead time: After firing, they take a while to reset, to be able to fire again. The dead time can outweigh the cost of the beginning of the experiment.
