You might remember that about one month ago, Nicole blogged about the conference Beyond i.i.d. in information theory and told us about bits, bears, and beyond in Banff. I was very pleased that Nicole did so, because this conference has become one of my favorites in recent years (ok, it’s my favorite). You can look at her post to see what is meant by “Beyond i.i.d.” The focus of the conference includes cutting-edge topics in quantum Shannon theory, and the conference still has a nice “small world” feel to it (for example, the most recent edition and the first one featured a music session from participants). Here is a picture of some of us having a fun time:
The Beyond i.i.d. series has shaped a lot of the research going on in this area and has certainly affected my own research directions. The first Beyond i.i.d. was held in Cambridge, UK in January 2013, organized by Nilanjana Datta and Renato Renner. It had a clever logo, featuring cyclists of various sorts biking one after another, the first few looking the same and the ones behind them breaking out of the i.i.d. pattern:
It was also at the Cambridge edition that the famous entropy zoo first appeared, which has now been significantly updated, based on recent progress in the area. The next Beyond i.i.d. happened in Singapore in May 2014, organized by Marco Tomamichel, Vincent Tan, and Stephanie Wehner. (Stephanie was a recent “quantum woman” for her work on a loophole-free Bell experiment.)
The tradition continued this past summer in beautiful Banff, Canada. I hope that it goes on for a long time. At least I have next year’s to look forward to, which will be in beachy Barcelona in the summertime, (as of now) planned to be just one week before Alexander Holevo presents the Shannon lecture in Barcelona at the ISIT 2016 conference (by the way, this is the first time that a quantum information theorist has won the prestigious Shannon award).
So why am I blabbing on and on about the Beyond i.i.d. conference if Nicole already wrote a great summary of the Banff edition this past summer? Well, she didn’t have room in her blog post to cover one of my favorite topics that was discussed at my favorite conference, so she graciously invited me to discuss it here.
The driving question of my new favorite topic is “What is the right notion of a quantum Markov chain?” The past year or so has seen some remarkable progress in this direction. To motivate it, let’s go back to bears, and specifically bear attacks (as featured in Nicole’s post). In Banff, the locals there told us that they had never heard of a bear attacking a group of four or more people who hike together. But let’s suppose that Alice, Bob, and Eve ignore this advice and head out together for a hike in the mountains. Also, in a different group are 50 of Alice’s sisters, but the park rangers are focusing their binoculars on the group of three (Alice, Bob, and Eve), observing their movements, because they are concerned that a group of three will run into trouble.
In the distance, there is a clever bear observing the movements of Alice, Bob, and Eve, and he notices some curious things. If he looks at Alice and Bob’s movements alone, they appear to take each step randomly, but for the most part together. That is, their steps appear correlated. He records their movements for some time and estimates a probability distribution 
that characterizes their movements. However, if he considers the movements of Alice, Bob, and Eve all together, he realizes that Alice and Bob are really taking their steps based on what Eve does, who in turn is taking her steps completely at random. So at this point the bear surmises that Eve is the mediator of the correlations observed between Alice and Bob’s movements, and when he writes down an estimate for the probability distribution 
characterizing all three of their movements, he notices that it factors as 
. That is, the bear sees that the distribution forms a Markov chain.
“What is an important property of such a Markov chain?“, asks the bear. Well, neglecting Alice’s movements (summing over the 
variable), the probability distribution reduces to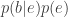 
, because 
is a conditional probability distribution. A characteristic of a Markov probability distribution is that one could reproduce the original distribution simply by acting on the 
variable of 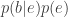with the conditional probability distribution . So the bear realizes that it would be possible for Alice to be lost and subsequently replaced by Eve calling in one of Alice’s sisters, such that nobody else would notice anything different from before — it would appear as if the movements of all three were unchanged once this replacement occurs. Salivating at his realization, the bear takes Eve briefly aside without any of the others noticing. The bear explains that he will not eat Eve and will instead eat Alice if Eve can call in one of Alice’s sisters and direct her movements to be chosen according to the distribution . Eve, realizing that her options are limited (ok, ok, maybe there are other options…), makes a deal with the bear. So the bear promptly eats Alice, and Eve draws in one of Alice’s sisters, whom Eve then directs to walk according to the distribution . This process repeats, going on and on, and all the while, the park rangers, focusing exclusively on the movements on the party of three, don’t think anything of what’s going because they observe that the joint distribution describing the movements of “Alice,” Bob, and Eve never seems to change (let’s assume that the actions of the bear and Eve are very fast 🙂 ). So the bear is very satisfied after eating Alice and some of her sisters, and Eve is pleased not to be eaten, at the same time never having cared too much for Alice or any of her sisters.
A natural question arises: “What could Alice and Bob do to prevent this terrible situation from arising, in which Alice and so many of her sisters get eaten without the park rangers noticing anything?” Well, Alice and Bob could attempt to coordinate their movements independently of Eve’s. Even better, before heading out on a hike, they could make sure to have brought along several entangled pairs of particles (and perhaps some bear spray). If Alice and Bob choose their movements according to the outcomes of measurements of the entangled pairs, then it would be impossible for Alice to be eaten and the park rangers not to notice. That is, the distribution describing their movements could never be described by a Markov chain distribution of the form 
. Thus, in such a scenario, as soon as the bear attacks Alice and then Eve replaces her with one of her sisters, the park rangers would immediately notice something different about the movements of the party of three and then figure out what is going on. So at least Alice could save her sisters…
What is the lesson here? A similar scenario is faced in quantum key distribution. Eve and other attackers (such as a bear) might try to steal what is there in Alice’s system and then replace it with something else, in an attempt to go undetected. If the situation is described by classical physics, this would be possible if Eve had access to a “hidden variable” that dictates the actions of Alice and Bob. But according to Bell’s theorem or the monogamy of entanglement, it is impossible for a “hidden variable” strategy to mimic the outcomes of measurements performed on sufficiently entangled particles.
Since we never have perfectly entangled particles or ones whose distributions exactly factor as Markov chains, it would be ideal to quantify, for a given three-party quantum state of Alice, Bob, and Eve, how well one could recover from the loss of the Alice system by Eve performing a recovery channel on her system alone. This would help us to better understand approximate cases that we expect to appear in realistic scenarios. At the same time, we could have a more clear understanding of what constitutes an approximate quantum Markov chain.
Now due to recent results of Fawzi and Renner, we know that this quantification of quantum non-Markovianity is possible by using the conditional quantum mutual information (CQMI), a fundamental measure of information in quantum information theory. We already knew that the CQMI is non-negative when evaluated for any three-party quantum state, due to the strong subadditivity inequality, but now we can say more than that: If the CQMI is small, then Eve can recover well from the loss of Alice, implying that the reduced state of Alice and Bob’s system could not have been too entangled in the first place. Relatedly, if Eve cannot recover well from the loss of Alice, then the CQMI cannot be small. The CQMI is the quantity underlying the squashed entanglement measure, which in turn plays a fundamental role in characterizing the performance of realistic quantum key distribution systems.
Since the original results of Fawzi and Renner appeared on the arXiv, this topic has seen much activity in “quantum information land.” Here are some papers related to this topic, which have appeared in the past year or so (apologies if I missed your paper!):
Renyi generalizations of the conditional quantum mutual information
Fidelity of recovery, geometric squashed entanglement, and measurement recoverability
Renyi squashed entanglement, discord, and relative entropy differences
Squashed entanglement, k-extendibility, quantum Markov chains, and recovery maps
Quantum Conditional Mutual Information, Reconstructed States, and State Redistribution
Multipartite quantum correlations and local recoverability
Monotonicity of quantum relative entropy and recoverability
Quantum Markov chains, sufficiency of quantum channels, and Renyi information measures
The Fidelity of Recovery is Multiplicative
Universal recovery map for approximate Markov chains
Recoverability in quantum information theory
Strengthened Monotonicity of Relative Entropy via Pinched Petz Recovery Map
Universal recovery from a decrease of quantum relative entropy
Some of the papers are admittedly that of myself and my collaborators, but hey!, please forgive me, I’ve been excited about the topic. We now know simpler proofs of the original Fawzi–Renner results and extensions of them that apply to the quantum relative entropy as well. Since the quantum relative entropy is such a fundamental quantity in quantum information theory, some of the above papers provide sweeping ramifications for many foundational statements in quantum information theory, including entanglement theory, quantum distinguishability, the Holevo bound, quantum discord, multipartite information measures, etc. Beyond i.i.d. had a day of talks dedicated to the topic, and I think we will continue seeing further developments in this area.
The quantum world offers lots of scope for enthralling characters and mind-blowing plot twists, according to Artur Ekert, director of the Centre for Quantum Technologies and co-inventor of quantum cryptography. “A writer has plenty to play with when science allows things to be in two places – or even two universes – at once,” he says. “The result might be funny, tense or even confusing. But it certainly won’t be boring.” Artur is one of the Open category judges.
cannot transform into a state 
: 
. An ancilla 
, called a catalyst, might facilitate the transformation: 
. Catalysts act like engines used to extract work from a pair of heat baths.
, wherein 
resembles 
Quantum Frontiers 