It’s always exciting when you can bridge two different physical concepts that seem to have nothing in common—and it’s even more thrilling when the results have as broad a range of possible fields of application as from fault-tolerant quantum computation to quantum gravity.
Physicists love to draw connections between distinct ideas, interconnecting concepts and theories to uncover new structure in the landscape of scientific knowledge. Put together information theory with quantum mechanics and you’ve opened a whole new field of quantum information theory. More recently, machine learning tools have been combined with many-body physics to find new ways to identify phases of matter, and ideas from quantum computing were applied to Pozner molecules to obtain new plausible models of how the brain might work.
In a recent contribution, my collaborators and I took a shot at combining the two physical concepts of quantum error correction and physical symmetries. What can we say about a quantum error-correcting code that conforms to a physical symmetry? Surprisingly, a continuous symmetry prevents the code from doing its job: A code can conform well to the symmetry, or it can correct against errors accurately, but it cannot do both simultaneously.
By a continuous symmetry, we mean a transformation that is characterized by a set of continuous parameters, such as angles. For instance, if I am holding an atom in my hand (more realistically, it’ll be confined in some fancy trap with lots of lasers), then I can rotate it around and about in space:

A rotation like this is fully specified by an axis and an angle, which are continuous parameters. Other transformations that we could think of are, for instance, time evolution, or a continuous family of unitary gates that we might want to apply to the system.
On the other hand, a code is a way of embedding some logical information into physical systems:

By cleverly distributing the information that we care about over several physical systems, an error-correcting code is able to successfully recover the original logical information even if the physical systems are exposed to some noise. Quantum error-correcting codes are particularly promising for quantum computing, since qubits tend to lose their information really fast (current typical ones can hold their information for a few seconds). In this way, instead of storing the actual information we care about on a single qubit, we use extra qubits which we prepare in a complicated state that is designed to protect this information from the noise.
Covariant codes for quantum computation
A code that is compatible with respect to a physical symmetry is called covariant. This property ensures that if I apply a symmetry transformation on the logical information, this is equivalent to applying corresponding symmetry transformations on each of the physical systems.
Suppose I would like to flip my qubit from “0” to “1” and from “1” to “0”. If my information is stored in an encoded form, then in principle I first need to decode the information to uncover the original logical information, apply the flip operation, and then re-encode the new logical information back onto the physical qubits. A covariant code allows to perform the transformation directly on the physical qubits, without having to decode the information first:

The advantage of this scheme is that the logical information is never exposed and remains protected all along the computation.
But here’s the catch: Eastin and Knill famously proved that error-correcting codes can be at most covariant with respect to a finite set of transformations, ruling out universal computation with transversal gates. In other words, the computations we can perform using this scheme are very limited because we can’t perform any continuous symmetry transformation.
Interestingly, however, there’s a loophole: If we consider macroscopic systems, such as a particle with a very large value of spin, then it becomes possible again to construct codes that are covariant with respect to continuous transformations.
How is that possible, you ask? How do we transition from the microscopic regime, where covariant codes are ruled out for continuous symmetries, to the macroscopic regime, where they are allowed? We provide an answer by resorting to approximate quantum error correction. Namely, we consider the situation where the code does not have to correct each error exactly, but only has to reconstruct a good approximation of the logical information. As it turns out, there is a quantitative limit to how accurately a code can correct against errors if it is covariant with respect to a continuous symmetry, represented by the following equation:

where ![]() specifies how inaccurately the code error-corrects (
specifies how inaccurately the code error-corrects (![]() means the code can correct against errors perfectly), n is the number of physical subsystems, and the
means the code can correct against errors perfectly), n is the number of physical subsystems, and the ![]() and
and ![]() are measures of “how strongly” the symmetry transformation can act on the logical and physical subsystems.
are measures of “how strongly” the symmetry transformation can act on the logical and physical subsystems.
Let’s try to understand the right-hand side of this equation. In physics, continuous symmetries are generated by what we call physical charges. These are physical quantities that are associated with the symmetry, and that characterize how the symmetry acts on each state of the system. For instance, the charge that corresponds to time evolution is simply energy: States that label high energies have a rapidly varying phase whereas the phase of low-energy states changes slowly in time. Above, we indicate by ![]() the range of possible charge values on the logical system and by
the range of possible charge values on the logical system and by ![]() the corresponding range of charge values on each physical subsystem. In typical settings, this range of charge values is related to the dimension of the system—the more states the system has, intuitively, the greater range of charges it can accommodate.
the corresponding range of charge values on each physical subsystem. In typical settings, this range of charge values is related to the dimension of the system—the more states the system has, intuitively, the greater range of charges it can accommodate.
The above equation states that the inaccuracy of the code must be larger than some value given on the right-hand side of the equation, which depends on the number of subsystems n and the ranges of charge values on the logical system and physical subsystems. The right-hand side becomes small in two regimes: if each subsystem can accommodate a large range of charge values, or if there is a large number of physical systems. In these regimes, our limitation vanishes, and we can circumvent the Eastin-Knill theorem and construct good covariant error-correcting codes. This allows us to connect the two regimes that seemed incompatible earlier, the microscopic regime where there cannot be any covariant codes, and the macroscopic regime where they are allowed.
From quantum computation to many-body physics and quantum gravity
Quantum error-correcting codes not only serve to protect information in a quantum computation against noise, but they also provide a conceptual toolbox to understand complex physical systems where a quantum state is delocalized over many physical subsystems. The tight connections between quantum error correction and many-body physics have been put to light following a long history of pioneering research at Caltech in these fields. And as if that weren’t enough, quantum error correcting codes were also shown to play a crucial role in understanding quantum gravity.
There is an abundance of natural physical symmetries to consider both in many-body physics and in quantum gravity, and that gives us a good reason to be excited about characterizing covariant codes. For instance, there are natural approximate quantum error correcting codes that appear in some statistical mechanical models by cleverly picking global energy eigenstates. These codes are covariant with respect to time evolution by construction, since the codewords are energy eigenstates. Now, we understand more precisely under which conditions such codes can be constructed.
Perhaps an even more illustrative example is that of time evolution in holographic quantum gravity, that is, in the AdS/CFT correspondence. This model of quantum gravity has the property that it is equivalent to a usual quantum field theory that lives on the boundary of the universe. What’s more, the correspondence which tells us how the bulk quantum gravity theory is mapped to the boundary is, in fact, a quantum error-correcting code. If we add a time axis, then the picture becomes a cylinder where the interior is the theory of quantum gravity, and where the cylinder itself represents a traditional quantum field theory:
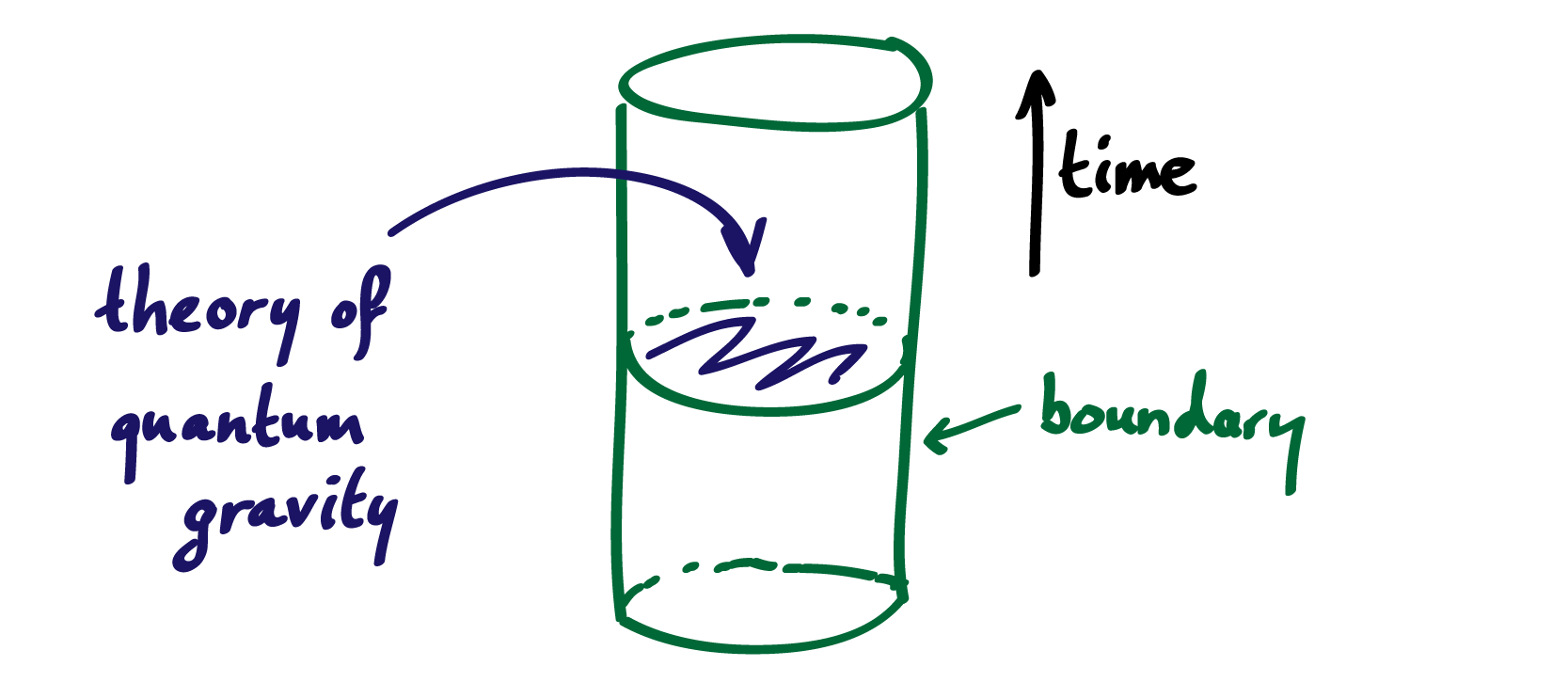
Since the bulk theory and the boundary theory are equivalent, the action of time evolution must be faithfully represented in both pictures. But this is in apparent contradiction with the Eastin-Knill theorem, from which it follows that a quantum error-correcting code cannot be covariant with respect to a continuous symmetry. We now understand how this is, in fact, not a contradiction: As we’ve seen, codes may be covariant with respect to continuous symmetries in the presence of systems with a large number of degrees of freedom, such as a quantum field theory.
What’s next?
There are some further results in our paper that I have not touched upon in this post, including a precise approximate statement of the Eastin-Knill theorem in terms of system dimensions, and a fun machinery to construct covariant codes for more general systems such as oscillators and rotors.
We have only scratched the surface of the different applications I’ve mentioned, by studying the properties of covariant codes in general. I’m now excited to dive into more detail with our wonderful team to study deeper applications to correlations in many-body systems, global symmetries in quantum gravity, accuracy limits of quantum clocks and precision limits to quantum metrology in the presence of noise.
This has been an incredibly fun project to work on. Such a collaboration illustrates again the benefit of interacting with great scientists with a wide range of areas of expertise including representation theory, continuous variable systems, and quantum gravity. Thanks Sepehr, Victor, Grant, Fernando, Patrick, and John, for this fantastic experience.





