A great childhood memory that I have comes from first playing “The Incredible Machine” on PC in the early 90’s. For those not in the know, this is a physics-based puzzle game about building Rube Goldberg style contraptions to achieve given tasks. What made this game a standout for me was the freedom that it granted players. In many levels you were given a disparate set of components (e.g. strings, pulleys, rubber bands, scissors, conveyor belts, Pokie the Cat…) and it was entirely up to you to “MacGuyver” your way to some kind of solution (incidentally, my favorite TV show from that time period). In other words, it was often a creative exercise in designing your own solution, rather than “connecting the dots” to find a single intended solution. Growing up with games like this undoubtedly had significant influence in directing me to my profession as a research scientist: a job which is often about finding novel or creative solutions to a task given a limited set of tools.

From the late 90’s onwards puzzle games like “The Incredible Machine” largely went out of fashion as developers focused more on 3D games that exploited that latest hardware advances. However, this genre saw a resurgence in 2010’s spearheaded by developer “Zachtronics” who released a plethora of popular, and exceptionally challenging, logic and programming based puzzle games (some of my favorites include Opus Magnum and TIS-100). Zachtronics games similarly encouraged players to solve problems through creative designs, but also had the side-effect of helping players to develop and practice tangible programming skills (e.g. design patterns, control flow, optimization). This is a really great way to learn, I thought to myself.

So, fast-forward several years, while teaching undergraduate/graduate quantum courses at Georgia Tech I began thinking about whether it would be possible to incorporate quantum mechanics (and specifically quantum circuits) into a Zachtronics-style puzzle game. My thinking was that such a game might provide an opportunity for students to experiment with quantum through a hands-on approach, one that encouraged creativity and self-directed exploration. I was also hoping that representing quantum processes through a visual language that emphasized geometry, rather than mathematical language, could help students develop intuition in this setting. These thoughts ultimately led to the development of The Qubit Factory. At its core, this is a quantum circuit simulator with a graphic interface (not too dissimilar to the Quirk quantum circuit simulator) but providing a structured sequence of challenges, many based on tasks of real-life importance to quantum computing, that players must construct circuits to solve.

Quantum Gamification and The Qubit Factory

My goal in designing The Qubit Factory was to provide an accurate simulation of quantum mechanics (although not necessarily a complete one), such that players could learn some authentic, working knowledge about quantum computers and how they differ from regular computers. However, I also wanted to make a game that was accessible to the layperson (i.e. without a prior knowledge of quantum mechanics or the underlying mathematical foundations like linear algebra). These goals, which are largely opposing one-another, are not easy to balance!

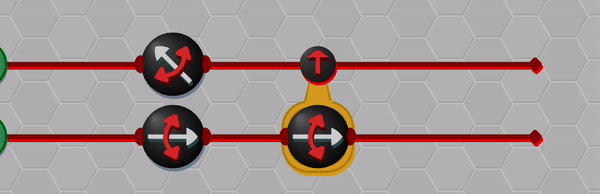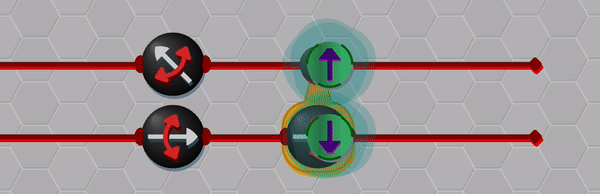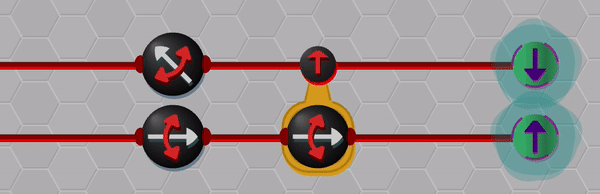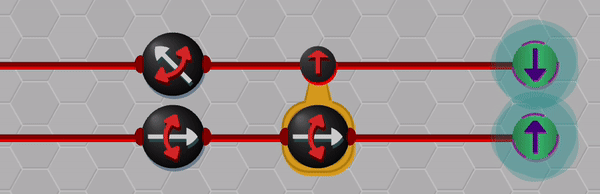
A key step in achieving this balance was to find a suitable visual depiction of quantum states and processes; here the Bloch sphere, which provides a simple geometric representation of qubit states, was ideal. However, it is also here that I made my first major compromise to the scope of the physics within the game by restricting the game state to real-valued wave-functions (which in turn implies that only gates which transform qubits within the X-Z plane can be allowed). I feel that this compromise was ultimately the correct choice: it greatly enhanced the visual clarity by allowing qubits to be represented as arrows on a flat disk rather than on a sphere, and similarly allowed the action of single-qubit gates to depicted clearly (i.e. as rotations and flips on the disk). Some purists may object to this limitation on grounds that it prevents universal quantum computation, but my counterpoint would be that there are still many interesting quantum tasks and algorithms that can be performed within this restricted scope. In a similar spirit, I decided to forgo the standard quantum circuit notation: instead I used stylized circuits to emphasize the geometric interpretation as demonstrated in the example below. This choice was made with the intention of allowing players to infer the action of gates from the visual design alone.

Okay, so while the Bloch sphere provides a nice way to represent (unentangled) single qubit states, we also need a way to represent entangled states of multiple qubits. Here I made use of some creative license to show entangled states as blinking through the basis states. I found this visualization to work well for conveying simple states such as the singlet state presented below, but players are also able to view the complete list of wave-function amplitudes if necessary.

Although the blinking effect is not a perfect solution for displaying superpositions, I think that it is useful in conveying key aspects like uncertainty and correlation. The animation below shows an example of the entangled wave-function collapsing when one of the qubits is measured.

So, thus far, I have described a quantum circuit simulator with some added visual cues and animations, but how can this be turned into a game? Here, I leaned heavily on the existing example of Zachtronic (and Zachtronic-like) games: each level in The Qubit Factory provides the player with some input bits/qubits and requires the player to perform some logical task in order to produce a set of desired outputs. Some of the levels within the game are highly structured, similar to textbook exercises. They aim to teach a specific concept and may only have a narrow set of potential solutions. An example of such a structured level is the first quantum level (lvl QI.A) which tasks the player with inverting a sequence of single qubit gates. Of course, this problem would be trivial to those of you already familiar with quantum mechanics: you could use the linear algebra result together with the knowledge that quantum gates are unitary, so the Hermitian conjugate of each gate doubles as its inverse. But what if you didn’t know quantum mechanics, or even linear algebra? Could this problem be solved through logical reasoning alone? This is where I think that the visuals really help; players should be able to infer several key points from geometry alone:

• the inverse of a flip (or mirroring about some axis) is another equal flip.
• the inverse of a rotation is an equal rotation in the opposite direction.
• the last transformation done on each qubit should be the first transformation to be inverted.

So I think it is plausible that, even without prior knowledge in quantum mechanics or linear algebra, a player could not only solve the level but also grasp some important concepts (i.e. that quantum gates are invertible and that the order in which they are applied matters).

Many of the levels in The Qubit Factory are also designed to be open-ended. Such levels, which often begin with a blank factory, have no single intended solution. The player is instead expected to use experimentation and creativity to design their own solution; this is the setting where I feel that the “game” format really shines. An example of an open-ended level is QIII.E, which gives the player 4 copies of a single qubit state , guaranteed to be either the or eigenstate, and tasks the player to determine which state they have been given. Those familiar with quantum computing will recognize this as a relatively simple problem in state tomography. There are many viable strategies that could be employed to solve this task (and I am not even sure of the optimal one myself). However, by circumventing the need for a mathematical calculation, the Qubit Factory allows players to easily and quickly explore different approaches. Hopefully this could allow players to find effective strategies through trial-and-error, gaining some understanding of state tomography (and why it is challenging) in the process.

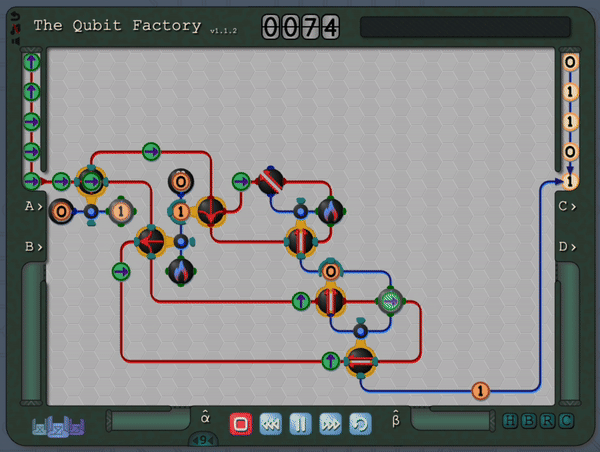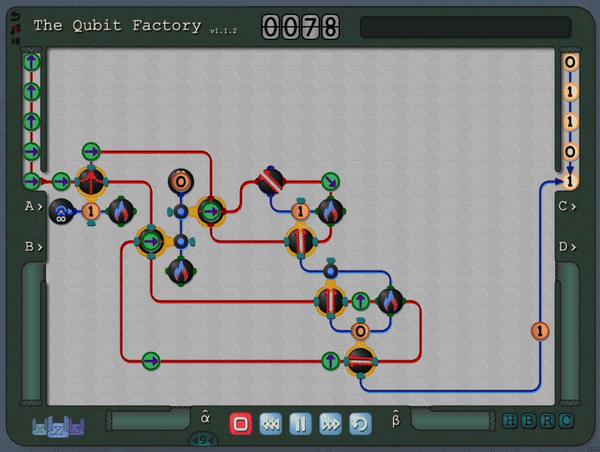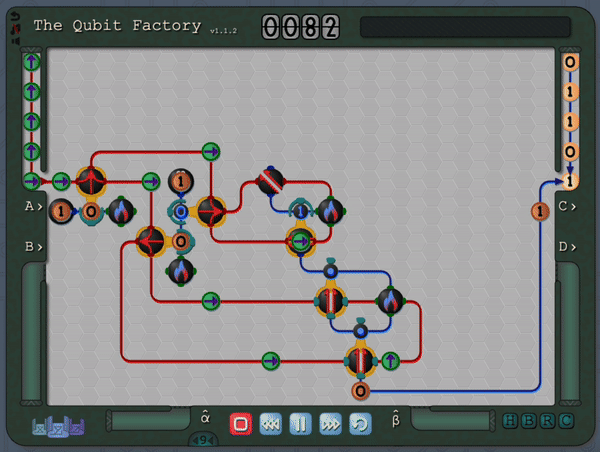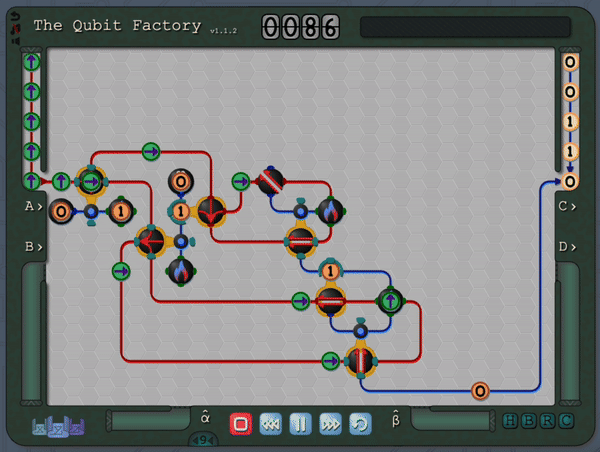
The Qubit Factory begins with levels covering the basics of qubits, gates and measurements. It later progresses to more advanced concepts like superpositions, basis changes and entangled states. Finally it culminates with levels based on introductory quantum protocols and algorithms (including quantum error correction, state tomography, super-dense coding, quantum repeaters, entanglement distillation and more). Even if you are familiar with the aforementioned material you should still be in for a substantial challenge, so please check it out if that sounds like your thing!

The Potential of Quantum Games

I believe that interactive games have great potential to provide new opportunities for people to better understand the quantum realm (a position shared by the IQIM, members of which have developed several projects in this area). As young children, playing is how we discover the world around us and build intuition for the rules that govern it. This is perhaps a significant reason why quantum mechanics is often a challenge for new students to learn; we don’t have direct experience or intuition with the quantum world in the same way that we do with the classical world. A quote from John Preskill puts it very succinctly:

“Perhaps kids who grow up playing quantum games will acquire a visceral understanding of quantum phenomena that our generation lacks.”

The Qubit Factory can be played at www.qubitfactory.io