This is a story about distillation—a process that has kept my family busy for generations.

My great, great, great, great grandfather was known as Brännvinskungen, loosely translated as the Vodka King. This “royal” ancestor of mine lived in the deepest forests of Småland, Sweden; the forests that during his time would populate the US state of Minnesota with emigrants fleeing the harshest lands of Europe. The demand for alcoholic beverages among their inhabitants was great. And the Vodka King had refined both his recipe and the technology to meet the demand. He didn’t claim to compete with big Stockholm-based companies in terms of quality or ambition. Nevertheless, his ability to, using simple means and low cost, turn water into (fortified) wine earned him his majestic title.

I’m not about to launch the concept of quantum vodka. Instead, I’m about to tell you about my and my stellar colleagues’ results on the distillation of quantum particles. In the spirit of the Vodka King, I don’t intend to compete with the big players of quantum computing. Instead, I will describe how a simple and low-cost method can distil information in quantum particles and improve technologies for measurements of physical things. Before I tell you about how quantum distillation can improve measurements, I need to explain why anyone would use quantum physics to do measurements in the first place, something known as quantum metrology.

According to Wikipedia, “metrology is the scientific study of measurement”. And just about any physical experiment or technology relies on measurements. Quantum metrology is the field of using quantum phenomena, such as entanglement, to improve measurements [1]. The ability to quantum-boost technologies for measurements has fostered a huge interest in quantum metrology. My hope is that speedometers, voltmeters, GPS devices and clocks will be improved by quantum metrology in the near future. 

There are some problems to overcome before quantum metrology will make it to the mainstream. Just like our eyes on a bright day, quantum-measurement devices saturate (are blinded) if they are subjected to overly intense beams of quantum particles. Very often the particle detectors are the limiting factor in quantum metrology: one can prepare incredibly strong beams of quantum particles, but one cannot detect and access all the information they contain. To remedy this, one could use lower-intensity beams, or insert filters just before the detectors. But ideally, one would distil the information from a large number of particles into a few, going from high to low intensity without losing any information. 

Collaborators and I have developed a quantum filter that solves this precise problem [2, 3]. (See this blog post for more details on our work.) Our filter provides sunglasses for quantum-metrology technologies. However, unlike normal sunglasses, our quantum filters increase the information content of the individual particles that pass through them. Figure 1 compares sunglasses (polarising and non-polarising) with our quantum filter; miniature bottles represent light-particles, and their content represents information.

• The left-most boxes show the effect of non-polarising sunglasses, which can be used when there is a strong beam of different types of light particles that carry different amounts of information. The sunglasses block a fraction of the light particles. This reduces glare and avoids eyes’ being blinded. However, information is lost with the blocked light particles. 
• When driving a car, you see light particles from the surroundings, which vibrate both horizontally and vertically. The annoying glare from the road, however, is made of light particles which vibrate predominantly horizontally. In this scenario, vertical light carries more information than horizontal light. Polarising sunglasses (middle boxes) can help. Irritating horizontal light particles are blocked, but informative vertical ones aren’t. On the level of the individual particles, however, no distillation takes place; the information in a vertical light particle is the same before and after the filter.
• The right-most boxes show the workings of our quantum filter. In quantum metrology, often all particles are the same, and all carry a small amount of information. Our filter blocks some particles, but compresses their information into the particles that survive the filter. The number of particles is reduced, but the information isn’t.

Our filter is not only different to sunglasses, but also to standard distillation processes. Distillation of alcohol has a limit: 100%. Given 10 litres of 10% wine, one could get at most 1 litre of 100% alcohol, not ½ litres of 200% alcohol. Our quantum filters are different. There is no cap on how much information can be distilled into a few particles; the information of a million particles can all be compressed into a single quantum particle. This exotic feature relies on negativity [4]. Quantum things cannot generally be described by probabilities between 0% and 100%, sometimes they require the exotic occurrence of negative probabilities. Experiments whose explanations require negative probabilities are said to possess negativity. 

In a recent theory-experiment collaboration, spearheaded by Aephraim Steinberg’s quantum-optics group, our multi-institutional team designed a measurement device that can harness negativity [5]. Figure 2 shows an artistic model of our technology. We used single light particles to measure the optical rotation induced by a piece of crystal. Light particles were created by a laser, and then sent through the crystal. The light particles were rotated by the crystal: information about the degree of rotation was encoded in the particles. By measuring these particles, we could access this information and learn what the rotation was. In Figure 2(a) the beam of particles is too strong, and the detectors do not work properly. Thus, we insert our quantum filter [Figure 2(b)]. Every light particle that passed our quantum filter carried the information of over 200 blocked particles. In other words, the number of particles that reached our detector was 200 times less, but the information the detector received stayed constant. This allowed us to measure the optical rotation to a level impossible without our filter. 

Our ambition is that our proof-of-principle experiment will lead to the development of filters for other measurements, beyond optical rotations. Quantum metrology with light particles is involved in technologies ranging from quantum-computer calibration to gravitational-wave detection, so the possibilities for our metaphorical quantum vodka are many.

David Arvidsson-Shukur, Cambridge (UK), 14 April 2022

David is a quantum researcher at the Hitachi Cambridge Laboratory. His research focuses on both fundamental aspects of quantum phenomena, and on practical aspects of bringing such phenomena into technologies.

[1] ‘Advances in quantum metrology’, V. Giovannetti, S. Lloyd, L. Maccone, Nature photonics, 5, 4, (2011), https://www.nature.com/articles/nphoton.2011.35

[2] ‘Quantum Advantage in Postselected Metrology’, D. R. M. Arvidsson-Shukur, N. Yunger Halpern, H. V. Lepage, A. A. Lasek, C. H. W. Barnes, and S. Lloyd, Nature Communications, 11, 3775 (2020), https://doi.org/10.1038/s41467-020-17559-w

[3] ‘Quantum Learnability is Arbitrarily Distillable’, J. Jenne, D. R. M. Arvidsson-Shukur, arXiv, (2020), https://arxiv.org/abs/2104.09520

[4] ‘Conditions tighter than noncommutation needed for nonclassicality’, D. R. M. Arvidsson-Shukur, J. Chevalier Drori, N. Yunger Halpern, J. Phys. A: Math. Theor., 54, 284001, (2021), https://iopscience.iop.org/article/10.1088/1751-8121/ac0289

[5] ‘Negative quasiprobabilities enhance phase-estimation in quantum-optics experiment’, N. Lupu-Gladstein, Y. B. Yilmaz, D. R. M. Arvidsson-Shukur, A. Broducht, A. O. T. Pang, Æ. Steinberg, N. Yunger Halpern, P.R.L (in production), (2022), https://arxiv.org/abs/2111.01194

Over the last few decades, transistor density has become so high that classical computers have run into problems with some of the quirks of quantum mechanics. Quantum computers, on the other hand, exploit these quirks to revolutionize the way computers work. They promise secure communications, simulation of complex molecules, ultrafast computations, and much more. The fear of being left behind as this new technology develops is now becoming pervasive around the world. As a result, there are large, near-term investments in developing quantum technologies, with parallel efforts aimed at attracting young people into the field of quantum information science and engineering in the long-term.

I was not surprised then that, after completing my master’s thesis in quantum optics at TU Berlin in Germany, I was invited to participate in a program called Quanten 1×1 and hosted by the Junge Tueftler (Young Tinkerers) non-profit, to get young people excited about quantum technologies. As part of a small team, we decided to develop tabletop games to explain the concepts of superposition, entanglement, quantum gates, and quantum encryption. In the sections that follow, I will introduce the thought process that led to the design of one of the final products on quantum encryption. If you want to learn more about the other games, you can find the relevant links at the end of this post.

The price of admission into the quantum realm

How much quantum mechanics is too much? Is it enough for people to know about the health of Schrödinger’s cat, or should we use a squishy ball with a smiley face and an arrow on it to get people excited about qubits and the Bloch sphere? In other words, what is the best way to go beyond metaphors and start delving into the real stuff? After all, we are talking about cutting-edge quantum technology here, which requires years of study to understand. Even the quantum experts I met with during the project had a hard time explaining their work to lay people.

Since there is no standardized way to explain these topics outside a university, the goal of our project was to try different models to teach quantum phenomena and make the learning as entertaining as possible. Compared to methods where people passively absorb the information, our tabletop-games approach leverages people’s curiosity and leads to active learning through trial and error.

A wooden quantum key generator (BB84)

Everybody has secrets

Most of the (sensitive) information that is transmitted over the Internet is encrypted. This means that only those with the right “secret key” can unlock the digital box and read the private message within. Without the secret key used to decrypt, the message looks like gibberish – a series of random characters. To encrypt the billions of messages being exchanged every day (over 300 billion emails alone), the Internet relies heavily on public-key cryptography and so-called one-way functions. These mathematical functions allow one to generate a public key to be shared with everyone, from a private key kept to themselves. The public key plays the role of a digital padlock that only the private key can unlock. Anyone (human or computer) who wants to communicate with you privately can get a digital copy of your padlock (by copying it from a pinned tweet on your Twitter account, for example), put their private message inside a digital box provided by their favorite app or Internet communication protocol running behind the scenes, lock the digital box using your digital padlock (public-key), and then send it over to you (or, accidentally, to anyone else who may be trying to eavesdrop). Ingeniously, only the person with the private key (you) can open the box and read the message, even if everyone in the world has access to that digital box and padlock.

But there is a problem. Current one-way functions hide the private key within the public key in a way that powerful enough quantum computers can reveal. The implications of this are pretty staggering. Your information (bank account, email, bitcoin wallet, etc) as currently encrypted will be available to anyone with such a computer. This is a very serious issue of global importance. So serious indeed, that the President of the United States recently released a memo aimed at addressing this very issue. Fortunately, there are ways to fight quantum with quantum. That is, there are quantum encryption protocols that not even quantum computers can break. In fact, they are as secure as the laws of physics.

Quantum Keys

A popular way of illustrating how quantum encryption works is through single photon sources and polarization filters. In classroom settings, this often boils down to lasers and small polarizing filters a few meters apart. Although lasers are pretty cool, they emit streams of photons (particles of light), not single photons needed for quantum encryption. Moreover, measuring polarization of individual photons (another essential part of this process) is often very tricky, especially without the right equipment. In my opinion the concept of quantum mechanical measurement and the collapse of wave functions is not easily communicated in this way.

Inspired by wooden toys and puzzles my mom bought for me as a kid after visits to the dentist, I tried to look for a more physical way to visualize the experiment behind the famous BB84 quantum key distribution protocol. After a lot of back and forth between the drawing board and laser cutter, the first quantum key generator (QeyGen) was built. 

How does the box work?

Note: This short description leaves out some details. For a deeper dive, I recommend watching the tutorial video on our Youtube channel.

The quantum key generator (QeyGen) consists of an outer and an inner box. The outer box is used by the person generating the secret key, while the inner box is used by the person with whom they wish to share that key. The sender prepares a coin in one of two states (heads = 0, tails = 1) and inserts it either into slot 1 (horizontal basis), or slot 2 (vertical basis) of the outer box. The receiver then measures the state of the coin in one of the same two bases by sliding the inner box to the left (horizontal basis = 1) or right (vertical basis = 2). Crucially, if the bases to prepare and measure the coin match, then both sender and receiver get the same value for the coin. But if the basis used to prepare the coin doesn’t match the measurement basis, the value of the coin collapses into one of the two allowed states in the measurement basis with 50/50 chance. Because of this design, the box can be used to illustrate the BB84 protocol that allows two distant parties to create and share a secure encryption key.

Simulating the BB84 protocol

The following is a step by step tutorial on how to play out the BB84 protocol with the QeyGen. You can play it with two (Alice, Bob) or three (Alice, Bob, Eve) people. It is useful to know right from the start that this protocol is not used to send private messages, but is instead used to generate a shared private key that can then be used with various encryption methods, like the one-time pad, to send secret messages.

BB84 Protocol:

1. Alice secretly “prepares” a coin by inserting it facing-towards (0) or facing-away (1) from her into one of the two slots (bases) on the outer box. She writes down the value (0 or 1) and basis (horizontal or vertical) of the coin she just inserted.
2. (optional) Eve, the eavesdropper, tries to “measure” the coin by sliding the inner box left (horizontal basis) or right (vertical basis), before putting the coin back through the outer box without anyone noticing.
3. Bob then secretly measures the coin in a basis of his choice and writes down the value (0 or 1) and basis (horizontal and vertical) as well.
4. Steps 1 and 3 are then repeated several times. The more times Alice and Bob go through this process, the more secure their secret key will be.

Sharing the key while checking for eavesdroppers:

1. Alice and Bob publicly discuss which bases they used at each “prepare” and “measure” step, and cross out the values of the coin corresponding to the bases that didn’t match (about half of them on average; here, it would be rounds 1,3,5,6,7, and 11).
2. Then, they publicly announce the first few (or a random subset of the) values that survive the previous step (i.e. have matching bases; here, it is rounds 2 and 4). If the values match for each round, then it is safe to assume that there was no eavesdrop attack. The remaining values are kept secret and can be used as a secure key for further communication.
3. If the values of Alice and Bob don’t match, Eve must have measured the coin (before Bob) in the wrong basis (hence, randomizing its value) and put it back in the wrong orientation from the one Alice had originally chosen. Having detected Eve’s presence, Alice and Bob switch to a different channel of communication and try again.

Note that the more rounds Alice and Bob choose for the eavesdropper detection, the higher the chance that the channel of communication is secure, since N rounds that all return the same value for the coin mean a chance that Eve got lucky and guessed Alice’s inputs correctly. To put this in perspective, a 20-round check for Eve provides a 99.9999% guarantee of security. Of course, the more rounds used to check for Eve, the fewer secure bits are left for Alice and Bob to share at the end. On average, after a total of 2(N+M) rounds, with N rounds dedicated to Eve, we get an M-bit secret key.

What do people learn?

When we play with the box, we usually encounter three main topics that we discuss with the participants.

1. qm states and quantum particles: We talk about superposition of quantum particles and draw an analogy from the coin to polarized photons.
2. qm measurement and basis: We ask about the state of the coin and discuss how we actually define a state and a basis for a coin. By using the box, we emphasize that the measurement itself (in which basis the coin is observed) can directly affect the state of the coin and collapse its “wavefunction”.
3. BB84 protocol: After a little playtime of preparing and measuring the coin with the box, we introduce the steps to perform the BB84 protocol as described above. The penny-dropping moment (pun intended) often happens when the participants realize that a spy intervening between preparation and measurement can change the state of the coin, leading to contradictions in the subsequent eavesdrop test of the protocol and exposing the spy.

I hope that this small outline has provided a rough idea of how the box works and why we developed it. If you have access to a laser cutter, I highly recommend making a QeyGen for yourself (link to files below). For any further questions, feel free to contact me at t.schubert@fu-berlin.de.

Resources and acknowledgments

Project page Junge Tueftler: tueftelakademie.de/quantum1x1
Video series for the QeyGen: youtube.com/watch?v=YmdoAP1TJRo
Laser cut files: thingiverse.com/thing:5376516

The program was funded by the Federal Ministry of Education and Research (Germany) and was a collaboration between the Jungen Tueftlern and the Technical University of Berlin.
A special thanks to Robert from Project Sci.Com who helped me with the development.

I used to catch lizards—brown anoles, as I learned to call them later—as a child. They were colored as their name suggests, were about as long as one of my hands, and resented my attention. But they frequented our back porch, and I had a butterfly net. So I’d catch lizards, with my brother or a friend, and watch them. They had throats that occasionally puffed out, exposing red skin, and tails that detached and wriggled of their own accord, to distract predators.

Some theorists might appreciate butterfly nets, I imagine, for catching experimentalists. Some of us theorists will end a paper or a talk with “…and these predictions are experimentally accessible.” A pause will follow the paper’s release or the talk, in hopes that a reader or an audience member will take up the challenge. Usually, none does, and the writer or speaker retires to the Great Deck Chair of Theory on the Back Patio of Science.

So I was startled when an anole, metaphorically speaking, volunteered a superconducting qubit for an experiment I’d proposed.

The experimentalist is one of the few people I can compare to a reptile without fear that he’ll take umbrage: Kater Murch, an associate professor of physics at Washington University in St. Louis. The most evocative description of Kater that I can offer appeared in an earlier blog post: “Kater exudes the soberness of a tenured professor but the irreverence of a Californian who wears his hair slightly long and who tattooed his wedding band on.”

Kater expressed interest in an uncertainty relation I’d proved with theory collaborators. According to some of the most famous uncertainty relations, a quantum particle can’t have a well-defined position and a well-defined momentum simultaneously. Measuring the position disturbs the momentum; any later momentum measurement outputs a completely random, or uncertain, number. We measure uncertainties with entropies: The greater an entropy, the greater our uncertainty. We can cast uncertainty relations in terms of entropies.

I’d proved, with collaborators, an entropic uncertainty relation that describes chaos in many-particle quantum systems. Other collaborators and I had shown that weak measurements, which don’t disturb a quantum system much, characterize chaos. So you can check our uncertainty relation using weak measurements—as well as strong measurements, which do disturb quantum systems much. One can simplify our uncertainty relation—eliminate the chaos from the problem and even eliminate most of the particles. An entropic uncertainty relation for weak and strong measurements results.

Kater specializes in weak measurements, so he resolved to test our uncertainty relation. Physical Review Letters published the paper about our collaboration this month. Quantum measurements can not only create uncertainty, the paper shows, but also reduce it: Kater and his PhD student Jonathan Monroe used light to measure a superconducting qubit, a tiny circuit in which current can flow forever. The qubit had properties analogous to position and momentum (the spin’s z– and x-components). If the atom started with a well-defined “position” (the z-component) and the “momentum” (the x-component) was measured, the outcome was highly random; the total uncertainty about the two measurements was large. But if the atom started with a well-defined “position” (z-component) and another property (the spin’s y-component) was measured before the “momentum” (the x-component) was measured strongly, the total uncertainty was lower. The extra measurement was designed not to disturb the atom much. But the nudge prodded the atom enough, rendering the later “momentum” measurement (the x measurement) more predictable. So not only can quantum measurements create uncertainty, but gentle quantum measurements can also reduce it.

I didn’t learn only physics from our experiment. When I’d catch a lizard, I’d tip it into a tank whose lid contained a magnifying lens, and I’d watch the lizard. I didn’t trap Kater and Jonathan under a magnifying glass, but I did observe their ways. Here’s what I learned about the species experimentalus quanticus.

1) They can run experiments remotely when a pandemic shuts down campus: A year ago, when universities closed and cities locked down, I feared that our project would grind to a halt. But Jonathan twiddled knobs and read dials via his computer, and Kater popped into the lab for the occasional fixer-upper. Jonathan even continued his experiment from another state, upon moving to Texas to join his parents. And here we theorists boast of being able to do our science almost anywhere.

2) They speak with one less layer of abstraction than I: We often discussed, for instance, the thing used to measure the qubit. I’d call the thing “the detector.” Jonathan would call it “the cavity mode,” referring to the light that interacts with the qubit, which sits in a box, or cavity. I’d say “poh-tay-toe”; they’d say “poh-tah-toe”; but I’m glad we didn’t call the whole thing off.

3) Experiments take longer than expected—even if you expect them to take longer than estimated: Kater and I hatched the plan for this project during June 2018. The experiment would take a few months, Kater estimated. It terminated last summer.

4) How they explain their data: Usually in terms of decoherence, the qubit’s leaking of quantum information into its environment. For instance, to check that the setup worked properly, Jonathan ran a simple test that ended with a measurement. (Experts: He prepared a eigenstate, performed a Hadamard gate, and measured .) The measurement should have had a 50% chance of yielding and a 50% chance of yield . But the outcome dominated the trials. Why? Decoherence pushed the qubit toward toward . (Amplitude damping dominated the noise.)

5) Seeing one’s theoretical proposal turn into an experiment feels satisfying: Due to point (3), among other considerations, experiments aren’t cheap. The lab’s willingness to invest in the idea I’d developed with other theorists was heartening. Furthermore, the experiment pushed us to uncover more theory—for example, how tight the uncertainty bound could grow.

After getting to know an anole, I’d release it into our backyard and bid it adieu.¹ So has Kater moved on to experimenting with topology, and Jonathan has progressed toward graduation. But more visitors are wriggling in the Butterfly Net of Theory-Experiment Collaboration. Stay tuned.

¹Except for the anole I accidentally killed, by keeping it in the tank for too long. But let’s not talk about that.

I used to eat lunch at the foundations-of-quantum-theory table. 

I was a Masters student at the Perimeter Institute for Theoretical Physics, where I undertook a research project during the spring term. The project squatted on the border between quantum information theory and quantum foundations, where my two mentors worked. Quantum foundations concerns how quantum physics differs from classical physics; which alternatives to quantum physics could govern our world but don’t; and those questions, such as about Schrödinger’s cat, that fascinate us when we first encounter quantum theory, that many advisors warn probably won’t land us jobs if we study them, and that most physicists argue about only over a beer in the evening.

I don’t drink beer, so I had to talk foundations over sandwiches around noon.

One of us would dream up what appeared to be a perpetual-motion machine; then the rest of us would figure out why it couldn’t exist. Satisfied that the second law of thermodynamics still reigned, we’d decamp for coffee. (Perpetual-motion machines belong to the foundations of thermodynamics, rather than the foundations of quantum theory, but we didn’t discriminate.) I felt, at that lunch table, an emotion blessed to a student finding her footing in research, outside her country of origin: belonging.

The quantum-foundations lunch table came to mind last month, when I learned that Britain’s Institute of Physics had selected me to receive its International Quantum Technology Emerging Researcher Award. I was very grateful for the designation, but I was incredulous: Me? Technology? But I began grad school at the quantum-foundations lunch table. Foundations is to technology as the philosophy of economics is to dragging a plow across a wheat field, at least stereotypically.

Worse, I drag plows from wheat field to barley field to oat field. I’m an interdisciplinarian who never belongs in the room I’ve joined. Among quantum information theorists, I’m the thermodynamicist, or that theorist who works with experimentalists; among experimentalists, I’m the theorist; among condensed-matter physicists, I’m the quantum information theorist; among high-energy physicists, I’m the quantum information theorist or the atomic-molecular-and-optical (AMO) physicist; and, among quantum thermodynamicists, I do condensed matter, AMO, high energy, and biophysics. I usually know less than everyone else in the room about the topic under discussion. An interdisciplinarian can leverage other fields’ tools to answer a given field’s questions and can discover questions. But she may sound, to those in any one room, as though she were born yesterday. As Kermit the Frog said, 

Grateful as I am, I’d rather not dwell on why the Institute of Physics chose my file; anyone interested can read the citation or watch the thank-you speech. But the decision turned out to involve foundations and interdisciplinarity. So I’m dedicating this article to two sources of inspiration: an organization that’s blossomed by crossing fields and an individual who’s driven technology by studying fundamentals.

Britain’s Institute for Physics has a counterpart in the American Physical Society. The latter has divisions, each dedicated to some subfield of physics. If you belong to the society and share an interest in one of those subfields, you can join that division, attend its conferences, and receive its newsletters. I learned about Division of Soft Matter from this article, which I wish I could quote almost in full. This division’s members study “a staggering variety of materials from the everyday to the exotic, including polymers such as plastics, rubbers, textiles, and biological materials like nucleic acids and proteins; colloids, a suspension of solid particles such as fogs, smokes, foams, gels, and emulsions; liquid crystals like those found in electronic displays; [ . . . ] and granular materials.” Members belong to physics, chemistry, biology, engineering, and geochemistry. 

Despite, or perhaps because of, its interdisciplinarity, the division has thrived. The group grew from a protodivision (a “topical group,” in the society’s terminology) to a division in five years—at “an unprecedented pace.” Intellectual diversity has complemented sociological diversity: The division “ranks among the top [American Physical Society] units in terms of female membership.” The division’s chair observes a close partnership between theory and experiment in what he calls “a vibrant young field.”

And some division members study oobleck. Wouldn’t you like to have an excuse to say “oobleck” every day?

The second source of inspiration lives, like the Institute of Physics, in Britain. David Deutsch belongs at the quantum-foundations table more than I. A theoretical physicist at Oxford, David cofounded the field of quantum computing. He explained why to me in a fusion of poetry and the pedestrian: He was “fixing the roof” of quantum theory. As a graduate student, David wanted to understand quantum foundations—what happens during a measurement—but concluded that quantum theory has too many holes. The roof was leaking through those holes, so he determined to fix them. He studied how information transformed during quantum processes, married quantum theory with computer science, and formalized what quantum computers could and couldn’t accomplish. Which—years down the road, fused with others’ contributions—galvanized experimentalists to harness ions and atoms, improve lasers and refrigerators, and build quantum computers and quantum cryptography networks. 

David is a theorist and arguably a philosopher. But he’d have swept the Institute of Physics’s playing field, could he have qualified as an “emerging researcher” this autumn (David began designing quantum algorithms during the 1980s).

I returned to the Perimeter Institute during the spring term of 2019. I ate lunch at the quantum-foundations table, and I felt that I still belonged. I feel so still. But I’ve eaten lunch at other tables by now, and I feel that I belong at them, too. I’m grateful if the habit has been useful.

Congratulations to Hannes Bernien, who won the institute’s International Quantum Technology Young Scientist Award, and to the “highly commended” candidates, whom you can find here!

Sometimes, experimental results spark enormous curiosity inspiring a myriad of questions and ideas for further experimentation. In 2004, Geim and Novoselov, from The University of Manchester, isolated a single layer of graphene from bulk graphite with the “Scotch Tape Method” for which they were awarded the 2010 Nobel Prize in Physics.  This one experimental result has branched out countless times serving as a source of inspiration in as many different fields.  We are now in the midst of an array of branching-out in graphene research, and one of those branches gaining attention is ultra low friction observed between graphene and other surface materials.  

Much has been learned about graphene in the past 15 years through an immense amount of research, most of which, in non-mechanical realms (e.g., electron transport measurements, thermal conductivity, pseudo magnetic fields in strain engineering).  However, superlubricity, a mechanical phenomenon, has become the focus among many research groups. Mechanical measurements have famously shown graphene’s tensile strength to be hundreds of times that of the strongest steel, indisputably placing it atop the list of construction materials best for a superhero suit.  Superlubricity is a tribological property of graphene and is, arguably, as equally impressive as graphene’s tensile strength.

Tribology is the study of interacting surfaces during relative motion including sources of friction and methods for its reduction.  It’s not a recent discovery that coating a surface with graphite (many layers of graphene) can lower friction between two sliding surfaces.  Current research studies the precise mechanisms and surfaces for which to minimize friction with single or several layers of graphene. 

Research published in Nature Materials in 2018 measures friction between surfaces under constant load and velocity. The experiment includes two groups; one consisting of two graphene surfaces (homogeneous junction), and another consisting of graphene and hexagonal boron nitride (heterogeneous junction).   The research group measures friction using Atomic Force Microscopy (AFM).  The hexagonal boron nitride (or graphene for a homogeneous junction) is fixed to the stage of the AFM while the graphene slides atop.  Loads are held constant at 20 𝜇N and sliding velocity constant at 200 nm/s. Ultra low friction is observed for homogeneous junctions when the underlying crystalline lattice structures of the surfaces are at a relative angle of 30 degrees.  However, this ultra low friction state is very unstable and upon sliding, the surfaces rotate towards a locked-in lattice alignment. Friction varies with respect to the relative angle between the two surface’s crystalline lattice structures. Minimum (ultra low) friction occurs at a relative angle of 30 degrees reaching a maximum when locked-in lattice alignment is realized upon sliding. While in a state of lattice alignment, shearing is rendered impossible with the experimental setup due to the relatively large amount of friction.

Friction varies with respect to the relative angle of the crystalline lattice structures and is, therefore, anisotropic.  For example, the fact it takes less force to split wood when an axe blade is applied parallel to its grains than when applied perpendicularly illustrates the anisotropic nature of wood, as the force to split wood is dependent upon the direction along which the force is applied.  Frictional anisotropy is greater in homogeneous junctions because the tendency to orient into a stuck, maximum friction alignment, is greater than with heterojunctions.  In fact, heterogeneous junctions experience frictional anisotropy three orders of magnitude less than homogeneous junctions. Heterogenous junctions display much less frictional anisotropy due to a lattice misalignment when the angle between the lattice vectors is at a minimum.  In other words, the graphene and hBN crystalline lattice structures are never parallel because the materials differ, therefore, never experience the impact of lattice alignment as do homogenous junctions. Hence, heterogeneous junctions do not become stuck in a high friction state that characterizes homogeneous ones, and experience ultra low friction during sliding at all relative crystalline lattice structure angles.

Presumably, to increase applicability, upscaling to much larger loads will be necessary. A large scale cost effective method to dramatically reduce friction would undoubtedly have an enormous impact on a great number of industries.  Cost efficiency is a key component to the realization of graphene’s potential impact, not only as it applies to superlubricity, but in all areas of application.  As access to large amounts of affordable graphene increases, so will experiments in fabricating devices exploiting the extraordinary characteristics which have placed graphene and graphene based materials on the front lines of material research the past couple decades.

Xi Dong, Alex Maloney, Henry Maxfield and I recently posted a paper to the arXiv with the title: Phase Transitions in 3D Gravity and Fractal Dimension. In other words, we’ll get about ten readers per year for the next few decades. Despite the heady title, there’s deep geometrical beauty underlying this work. In this post I want to outline the origin story and motivation behind this paper.

There are two different branches to the origin story. The first was my personal motivation and the second is related to how I came into contact with my collaborators (who began working on the same project but with different motivation, namely to explain a phase transition described in this paper by Belin, Keller and Zadeh.)

During the first year of my PhD at Caltech I was working in the mathematics department and I had a few brief but highly influential interactions with Nikolai Makarov while I was trying to find a PhD advisor. His previous student, Stanislav Smirnov, had recently won a Fields Medal for his work studying Schramm-Loewner evolution (SLE) and I was captivated by the beauty of these objects.

SLE example from Scott Sheffield’s webpage. SLEs are the fractal curves that form at the interface of many models undergoing phase transitions in 2D, such as the boundary between up and down spins in a 2D magnet (Ising model.)

One afternoon, I went to Professor Makarov’s office for a meeting and while he took a brief phone call I noticed a book on his shelf called Indra’s Pearls, which had a mesmerizing image on its cover. I asked Professor Makarov about it and he spent 30 minutes explaining some of the key results (which I didn’t understand at the time.) When we finished that part of our conversation Professor Makarov described this area of math as “math for the future, ahead of the tools we have right now” and he offered for me to borrow his copy. With a description like that I was hooked. I spent the next six months devouring this book which provided a small toehold as I tried to grok the relevant mathematics literature. This year or so of being obsessed with Kleinian groups (the underlying objects in Indra’s Pearls) comes back into the story soon. I also want to mention that during that meeting with Professor Makarov I was exposed to two other ideas that have driven my research as I moved from mathematics to physics: quasiconformal mappings and the simultaneous uniformization theorem, both of which will play heavy roles in the next paper I release.  In other words, it was a pretty important 90 minutes of my life.

Google image search for “Indra’s Pearls”. The math underlying Indra’s Pearls sits at the intersection of hyperbolic geometry, complex analysis and dynamical systems. Mathematicians oftentimes call this field the study of “Kleinian groups”. Most of these figures were obtained by starting with a small number of Mobius transformations (usually two or three) and then finding the fixed points for all possible combinations of the initial transformations and their inverses. Indra’s Pearls was written by David Mumford, Caroline Series and David Wright. I couldn’t recommend it more highly.

My life path then hit a discontinuity when I was recruited to work on a DARPA project, which led to taking an 18 month leave of absence from Caltech. It’s an understatement to say that being deployed in Afghanistan led to extreme introspection. While “down range” I had moments of clarity where I knew life was too short to work on anything other than ones’ deepest passions. Before math, the thing that got me into science was a childhood obsession with space and black holes. I knew that when I returned to Caltech I wanted to work on quantum gravity with John Preskill. I sent him an e-mail from Afghanistan and luckily he was willing to take me on as a student. But as a student in the mathematics department, I knew it would be tricky to find a project that involved all of: black holes (my interest), quantum information (John’s primary interest at the time) and mathematics (so I could get the degree.)

I returned to Caltech in May of 2012 which was only two months before the Firewall Paradox was introduced by Almheiri, Marolf, Polchinski and Sully. It was obvious that this was where most of the action would be for the next few years so I spent a great deal of time (years) trying to get sharp enough in the underlying concepts to be able to make comments of my own on the matter. Black holes are probably the closest things we have in Nature to the proverbial bottomless pit, which is an apt metaphor for thinking about the Firewall Paradox. After two years I was stuck. I still wasn’t close to confident enough with AdS/CFT to understand a majority of the promising developments. And then at exactly the right moment, in the summer of 2014, Preskill tipped my hat to a paper titled Multiboundary Wormholes and Holographic Entanglement by Balasubramanian, Hayden, Maloney, Marolf and Ross. It was immediately obvious to me that the tools of Indra’s Pearls (Kleinian groups) provided exactly the right language to study these “multiboundary wormholes.” But despite knowing a bridge could be built between these fields, I still didn’t have the requisite physics mastery (AdS/CFT) to build it confidently.

Before mentioning how I met my collaborators and describing the work we did together, let me first describe the worlds that we bridged together.

3D Gravity and Universality

As the media has sensationalized to death, one of the most outstanding questions in modern physics is to discover and then understand a theory of quantum gravity.  As a quick aside, Quantum gravity is just a placeholder name for such a theory. I used italics because physicists have already discovered candidate theories, such as string theory and loop quantum gravity (I’m not trying to get into politics, just trying to demonstrate that there are multiple candidate theories). But understanding these theories — carrying out all of the relevant computations to confirm that they are consistent with Nature and then doing experiments to verify their novel predictions — is still beyond our ability. Surprisingly, without knowing the specific theory of quantum gravity that guides Nature’s hand, we’re still able to say a number of universal things that must be true for any theory of quantum gravity. The most prominent example being the holographic principle which comes from the entropy of black holes being proportional to the surface area encapsulated by the black hole’s horizon (a naive guess says the entropy should be proportional to the volume of the black hole; such as the entropy of a glass of water.) Universal statements such as this serve as guideposts and consistency checks as we try to understand quantum gravity.

It’s exceedingly rare to find universal statements that are true in physically realistic models of quantum gravity. The holographic principle is one such example but it pretty much stands alone in its power and applicability. By physically realistic I mean: 3+1-dimensional and with the curvature of the universe being either flat or very mildly positively curved.  However, we can make additional simplifying assumptions where it’s easier to find universal properties. For example, we can reduce the number of spatial dimensions so that we’re considering 2+1-dimensional quantum gravity (3D gravity). Or we can investigate spacetimes that are negatively curved (anti-de Sitter space) as in the AdS/CFT correspondence. Or we can do BOTH! As in the paper that we just posted. The hope is that what’s learned in these limited situations will back-propagate insights towards reality.

The motivation for going to 2+1-dimensions is that gravity (general relativity) is much simpler here. This is explained eloquently in section II of Steve Carlip’s notes here. In 2+1-dimensions, there are no “local”/”gauge” degrees of freedom. This makes thinking about quantum aspects of these spacetimes much simpler.

The standard motivation for considering negatively curved spacetimes is that it puts us in the domain of AdS/CFT, which is the best understood model of quantum gravity. However, it’s worth pointing out that our results don’t rely on AdS/CFT. We consider negatively curved spacetimes (negatively curved Lorentzian manifolds) because they’re related to what mathematicians call hyperbolic manifolds (negatively curved Euclidean manifolds), and mathematicians know a great deal about these objects. It’s just a helpful coincidence that because we’re working with negatively curved manifolds we then get to unpack our statements in AdS/CFT.

Multiboundary wormholes

Finding solutions to Einstein’s equations of general relativity is a notoriously hard problem. Some of the more famous examples include: Minkowski space, de-Sitter space, anti-de Sitter space and Schwarzschild’s solution (which describes perfectly symmetrical and static black holes.) However, there’s a trick! Einstein’s equations only depend on the local curvature of spacetime while being insensitive to global topology (the number of boundaries and holes and such.) If M is a solution of Einstein’s equations and is a discrete subgroup of the isometry group of 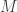, then the quotient space 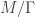will also be a spacetime that solves Einstein’s equations! Here’s an example for intuition. Start with 2+1-dimensional Minkowski space, which is just a stack of flat planes indexed by time. One example of a “discrete subgroup of the isometry group” is the cyclic group generated by a single translation, say the translation along the x-axis by ten meters. Minkowski space quotiented by this group will also be a solution of Einstein’s equations, given as a stack of 10m diameter cylinders indexed by time.

Start with 2+1-dimensional Minkowski space which is just a stack of flat planes index by time. Think of the planes on the left hand side as being infinite. To “quotient” by a translation means to glue the green lines together which leaves a cylinder for every time slice. The figure on the right shows this cylinder universe which is also a solution to Einstein’s equations.

D+1-dimensional Anti-de Sitter space (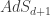) is the maximally symmetric d+1-dimensional Lorentzian manifold with negative curvature. Our paper is about 3D gravity in negatively curved spacetimes so our starting point is which can be thought of as a stack of Poincare disks (or hyperbolic sheets) with the time dimension telling you which disk (sheet) you’re on. The isometry group of is a group called which in turn is isomorphic to the group 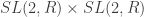. The group 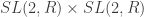isn’t a very common group but a single copy of 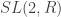is a very well-studied group. Discrete subgroups of it are called Fuchsian groups. Every element in the group should be thought of as a 2×2 matrix which corresponds to a Mobius transformation of the complex plane. The quotients that we obtain from these Fuchsian groups, or the larger isometry group yield a rich infinite family of new spacetimes, which are called multiboundary wormholes. Multiboundary wormholes have risen in importance over the last few years as powerful toy models when trying to understand how entanglement is dispersed near black holes (Ryu-Takayanagi conjecture) and for how the holographic dictionary works in terms of mapping operators in the boundary CFT to fields in the bulk (entanglement wedge reconstruction.)

Three dimensional AdS can be thought of as a stack of hyperboloids indexed by time. It’s convenient to use the Poincare disk model for the hyperboloids so that the entire spacetime can be pictured in a compact way. Despite how things appear, all of the triangles have the same “area”.

I now want to work through a few examples.

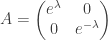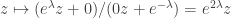BTZ black hole: this is the simplest possible example. It’s obtained by quotienting by a cyclic group , generated by a single matrix which for example could take the form . The matrix A acts by fractional linear transformation on the complex plane, so in this case the point gets mapped to . In this case

Start with as a stack of hyperbolic half planes indexed by time. A quotient by A means that each hyperbolic half plane gets quotiented. Quotienting a constant time slice by the map gives a surface that’s topologically a cylinder. Using the picture above this means you glue together the solid black curves. The green and red segments become two boundary regions. We call it the BTZ black hole because when you add “time” it becomes impossible to send a signal from the green boundary to the red boundary, or vica versa. The dotted line acts as an event horizon.

Three boundary wormhole: 

There are many parameterizations that we can choose to obtain the three boundary wormhole. I’ll only show schematically how the gluings go. A nice reference with the details is this paper by Henry Maxfield.

This is a picture of a constant time slice of quotiented by the A and B above. Each time slice is given as a copy of the hyperbolic half plane with the black arcs and green arcs glued together (by the maps A and B). These gluings yield a pair of pants surface. Each of the boundary regions are causally disconnected from the others. The dotted lines are black hole horizons that illustrate where the causal disconnection happens.

Torus wormhole: 

It’s simpler to write down generators for the torus wormhole; but following along with the gluings is more complicated. To obtain the three boundary wormhole we quotient by the free group where 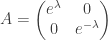 and 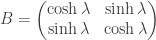. (Note that this is only one choice of generators, and a highly symmetrical one at that.)

This is a picture of a constant time slice of quotiented by the A and B above. Each time slice is given as a copy of the hyperbolic half plane with the black arcs and green arcs glued together (by the maps A and B). These gluings yield what’s called the “torus wormhole”. Topologically it’s just a donut with a hole cut out. However, there’s a causal structure when you add time to the mix where the dotted lines act as a black hole horizon, so that a message sent from behind the horizon will never reach the boundary.

Lorentzian to Euclidean spacetimes

So far we have been talking about negatively curved Lorentzian manifolds. These are manifolds that have a notion of both “time” and “space.” The technical definition involves differential geometry and it is related to the signature of the metric. On the other hand, mathematicians know a great deal about negatively curved Euclidean manifolds. Euclidean manifolds only have a notion of “space” (so no time-like directions.) Given a multiboundary wormhole, which by definition, is a quotient of 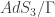where is a discrete subgroup of Isom(), there’s a procedure to analytically continue this to a Euclidean hyperbolic manifold of the form where is three dimensional hyperbolic space and is a discrete subgroup of the isometry group of , which is 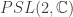. This analytic continuation procedure is well understood for time-symmetric spacetimes but it’s subtle for spacetimes that don’t have time-reversal symmetry. A discussion of this subtlety will be the topic of my next paper. To keep this blog post at a reasonable level of technical detail I’m going to need you to take it on a leap of faith that to every Lorentzian 3-manifold multiboundary wormhole there’s an associated Euclidean hyperbolic 3-manifold. Basically you need to believe that given a discrete subgroup of 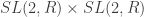 there’s a procedure to obtain a discrete subgroup of 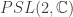. Discrete subgroups of  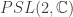are called Kleinian groups and quotients of by groups of this form yield hyperbolic 3-manifolds. These Euclidean manifolds obtained by analytic continuation arise when studying the thermodynamics of these spacetimes or also when studying correlation functions; there’s a sense in which they’re physical.

TLDR: you start with a 2+1-d Lorentzian 3-manifold obtained as a quotient 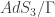and analytic continuation gives a Euclidean 3-manifold obtained as a quotient 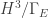where is 3-dimensional hyperbolic space and is a discrete subgroup of (Kleinian group.) 

Limit sets: 

Every Kleinian group 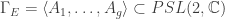has a fractal that’s naturally associated with it. The fractal is obtained by finding the fixed points of every possible combination of generators and their inverses. Moreover, there’s a beautiful theorem of Patterson, Sullivan, Bishop and Jones that says the smallest eigenvalue 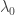of the spectrum of the Laplacian on the quotient Euclidean spacetime 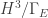is related to the Hausdorff dimension of this fractal (call it ) by the formula . This smallest eigenvalue controls a number of the quantities of interest for this spacetime but calculating it directly is usually intractable. However, McMullen proposed an algorithm to calculate the Hausdorff dimension of the relevant fractals so we can get at the spectrum efficiently, albeit indirectly.

This is a screen grab of Figure 2 from our paper. These are two examples of fractals that emerge when studying these spacetimes. Both of these particular fractals have a 3-fold symmetry. They have this symmetry because these particular spacetimes came from looking at something called “n=3 Renyi entropies”. The number q indexes a one complex dimensional family of spacetimes that have this 3-fold symmetry. These Kleinian groups each have two generators that are described in section 2.3 of our paper.

What we did

Our primary result is a generalization of the Hawking-Page phase transition for multiboundary wormholes. To understand the thermodynamics (from a 3d quantum gravity perspective) one starts with a fixed boundary Riemann surface and then looks at the contributions to the partition function from each of the ways to fill in the boundary (each of which is a hyperbolic 3-manifold). We showed that the expected dominant contributions, which are given by handlebodies, are unstable when the kinetic operator 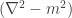is negative, which happens whenever the Hausdorff dimension of the limit set of is greater than the lightest scalar field living in the bulk. One has to go pretty far down the quantum gravity rabbit hole (black hole) to understand why this is an interesting research direction to pursue, but at least anyone can appreciate the pretty pictures!